Tenho um trabalho de Calculo 2 para entregar amanhã. 2 questões envolvem Derivadas Parciais para serem solucionadas, e está é a minha dificuldade.
Questão 1:
Uma placa metálica circular com centro na origem, possui a temperatura T no ponto (x,y) dada por T(x,y)=400*(2+x^2+3y^2)^-1 ºC
Qual a direção que se deve tomar a partir do ponto A(1,1) de modo que a temperatura aumente o mais rapido possivel e com que velocidade T(x,y) aumenta ao passar pelo ponto A nessa direção?
- Eu sei como resolver o problema, porem eu travo na parte que preciso derivar a Função T(x,y)=400*(2+x^2+3y^2)^1/2 em x e em y. HELP!
A outra questão é parecida assim e eu travo no mesmo momento que preciso derivar em x e em y.
Segue a outra Funções que preciso de ajuda na derivação parcial:
2: T(x,y) = 46-(140-x^2-3y^2)^1/2
Imagino que por serem funções compostas eu esteja com essa dificuldade.
EU FICAREI MUITO GRATO SE ALGUÉM PUDER ME AJUDAR HOJE AINDA, A ENTREGA DO TRABALHO É AMANHÃ.



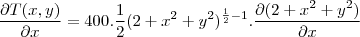
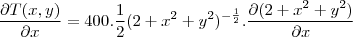
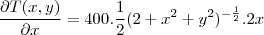








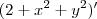
 tem como derivada
tem como derivada  portanto
portanto

 .
.



