 por nandooliver008 » Dom Nov 02, 2014 22:29
por nandooliver008 » Dom Nov 02, 2014 22:29
to em duvida na propriedade ||kv|| = |k| ||v|| na questão c)
a)encontre vetores em

de norma 1 cujo produto interno com vetor v= (3,-1) é zero.
b)mostre que existem infinitos vetores em

com norma 1 e cujo produto interno com vetor v= (1,-3,5) é zero.
c)sejá u=(4,1,2), v=(0,3,8), w=(3,1,2). obtenha as expressões.
||-2u|| + 2 ||u||
||3u-5v+w||
Na primeira tentei fazer ||(x,y)||=1 e 3x-1=0
Na c) meus resultados foram
![\sqrt[]{1414} \sqrt[]{1414}](/latexrender/pictures/09ba35ced1b0beb2af921c023811eeb6.png)
e

![\sqrt[]{21} \sqrt[]{21}](/latexrender/pictures/35158d18eb3e07732f7dae4efebf5adb.png)
-
nandooliver008
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Sáb Mai 17, 2014 23:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: c&t
- Andamento: cursando
 por Russman » Seg Nov 03, 2014 02:43
por Russman » Seg Nov 03, 2014 02:43
Vetores em R^2 normalizados são da forma

. Para que o PI seja nulo com o vetor

é preciso que
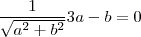
Ou seja,
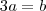
. Portanto, os vetores de R^2 normalizados perpendiculares ao vetor

são do tipo

Ou seja, na verdade a solução do problema é um único vetor.
Já para o caso do R^3 é diferente. Veja que o PI de

com

nulo gera

Ou seja, existem dois parâmetros livres a solução do problema. Logo, cada vetor

tal que

resolve o problema e existem infinitos trios a, b e c tais q isso ocorre.
Na c,
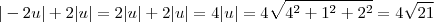
e
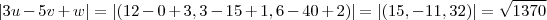
Se eu n errei nenhuma conta eu acredito q seja isso.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por nandooliver008 » Seg Nov 03, 2014 09:02
por nandooliver008 » Seg Nov 03, 2014 09:02
vlw cara muito obrigado mesmo.
-
nandooliver008
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Sáb Mai 17, 2014 23:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: c&t
- Andamento: cursando
 por nandooliver008 » Seg Nov 03, 2014 09:20
por nandooliver008 » Seg Nov 03, 2014 09:20
só mais uma duvida, pode me explicar porque em a-3b+5=0 existem 2 parâmetros? não entendi. vlw
-
nandooliver008
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Sáb Mai 17, 2014 23:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: c&t
- Andamento: cursando
 por nandooliver008 » Seg Nov 03, 2014 09:37
por nandooliver008 » Seg Nov 03, 2014 09:37
Russman escreveu:Vetores em R^2 normalizados são da forma

. Para que o PI seja nulo com o vetor

é preciso que
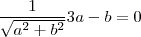
Ou seja,
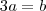
. Portanto, os vetores de R^2 normalizados perpendiculares ao vetor

são do tipo

Ou seja, na verdade a solução do problema é um único vetor.
Já para o caso do R^3 é diferente. Veja que o PI de

com

nulo gera

Ou seja, existem dois parâmetros livres a solução do problema. Logo, cada vetor

tal que

resolve o problema e existem infinitos trios a, b e c tais q isso ocorre.
Na c,
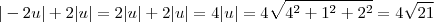
e
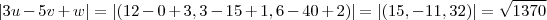
Se eu n errei nenhuma conta eu acredito q seja isso.
só mais uma duvida, pode me explicar porque em a-3b+5=0 existem 2 parâmetros? não entendi. vlw
-
nandooliver008
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Sáb Mai 17, 2014 23:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: c&t
- Andamento: cursando
 por Russman » Seg Nov 03, 2014 14:46
por Russman » Seg Nov 03, 2014 14:46
Digamos que você escolha fixar o valor de

para, por exemplo,

. Então,
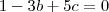
Ou seja, os valores de

e

ainda estão "amarrados" de modo que, para capturar um único vetor da forma prevista é preciso escolher duas coordenadas e calcular a terceira.
Entende?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Produto Interno Euclidiano
por ARCS » Sáb Dez 10, 2011 17:57
- 1 Respostas
- 2086 Exibições
- Última mensagem por MarceloFantini

Dom Dez 11, 2011 04:06
Geometria Analítica
-
- Produto Interno
por Claudin » Sáb Fev 16, 2013 15:50
- 2 Respostas
- 2456 Exibições
- Última mensagem por Claudin

Ter Fev 19, 2013 21:05
Álgebra Linear
-
- Produto Interno
por Claudin » Qua Fev 20, 2013 02:01
- 3 Respostas
- 2985 Exibições
- Última mensagem por LuizAquino

Qua Fev 20, 2013 10:27
Álgebra Linear
-
- Produto Interno
por iarapassos » Seg Mar 18, 2013 13:42
- 0 Respostas
- 1477 Exibições
- Última mensagem por iarapassos

Seg Mar 18, 2013 13:42
Álgebra Linear
-
- Produto Interno Usual
por iarapassos » Qui Mar 21, 2013 00:04
- 1 Respostas
- 1716 Exibições
- Última mensagem por Ge_dutra

Qui Mar 21, 2013 00:46
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 de norma 1 cujo produto interno com vetor v= (3,-1) é zero.
de norma 1 cujo produto interno com vetor v= (3,-1) é zero. com norma 1 e cujo produto interno com vetor v= (1,-3,5) é zero.
com norma 1 e cujo produto interno com vetor v= (1,-3,5) é zero.![\sqrt[]{1414} \sqrt[]{1414}](/latexrender/pictures/09ba35ced1b0beb2af921c023811eeb6.png) e
e 
![\sqrt[]{21} \sqrt[]{21}](/latexrender/pictures/35158d18eb3e07732f7dae4efebf5adb.png)


 . Para que o PI seja nulo com o vetor
. Para que o PI seja nulo com o vetor  é preciso que
é preciso que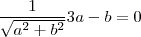
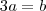 . Portanto, os vetores de R^2 normalizados perpendiculares ao vetor
. Portanto, os vetores de R^2 normalizados perpendiculares ao vetor 
 com
com  nulo gera
nulo gera
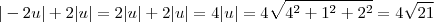
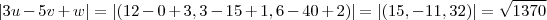

 para, por exemplo,
para, por exemplo,  . Então,
. Então,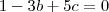
 e
e  ainda estão "amarrados" de modo que, para capturar um único vetor da forma prevista é preciso escolher duas coordenadas e calcular a terceira.
ainda estão "amarrados" de modo que, para capturar um único vetor da forma prevista é preciso escolher duas coordenadas e calcular a terceira.




