 por adauto martins » Sex Set 26, 2014 12:06
por adauto martins » Sex Set 26, 2014 12:06
meu caro pessoa estranha,
e o LATEX, nao consigo escrever certo...sai,mas num e bom...no caso,tomemos x1 diferente de x2 q. implica em suas imagens(y1 e y2) diferentes,caso de ser injetiva...no caso da sobrejetiva,mostrar-se q. para qquer y(imagem) existe um unico x do conj.dominio tal q. y=f(x),ou seja se tomarmos imagens iguais teremos dominios iguais o q. mostra q. os conjuntos domino e imagem teem os mesmo elementos,ou melhor sao iguais...vamos la...se tomarmos y=k,k um real,entao existe x,tal q. x e soluçao da equaçao dada,(x^3)+(x^2)+4x=k...obteremos x=f(k)...
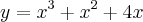


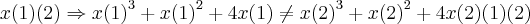 ,mostramos elementos distintos dos dois conj. terao imagens distintas,o q. prova a injeçao;agora podemos ver q. todo e qquer x tera sempre um y,e q. se tomarmos dois elementos de y(1) teremos os mesmos valores em y(2),ou seja os conj.imagens serao iguais,o q. prova a sobrejeçao...logo y e injetiva e sobrejetiva,o q.implica y injetiva
,mostramos elementos distintos dos dois conj. terao imagens distintas,o q. prova a injeçao;agora podemos ver q. todo e qquer x tera sempre um y,e q. se tomarmos dois elementos de y(1) teremos os mesmos valores em y(2),ou seja os conj.imagens serao iguais,o q. prova a sobrejeçao...logo y e injetiva e sobrejetiva,o q.implica y injetiva
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)