Tenho uma questão da FUVEST que diz assim:
A reta s passa pelo ponto (0,3) e é perpendicular à reta AB onde A=(0,0), e B é o centro da circinferência x²+y²-2x-4y=20. Então a equação de s é:
a)x-2y=-6
b) x+2y=6
c) x+y=3
d) y-x=3
e) 2x+y=6
A única forma de encontrar a resposta foi assim: y-yp=m.x-xp
y-3=-1/2.x-0
y-3=-x/2
x+2y=6 (B)
Mas pq ñão consigo achar resposta usando a fórmula do Raio da circinfeRência ( R= (raiz de Xc²+yc²-F) e então usar: (x-xc)²+(y+yc)²=R². Com esta fórmula não obterei a equação da reta?
Obrigada!



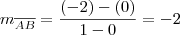
 é perpendicular à reta
é perpendicular à reta  , temos:
, temos:

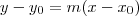 :
:
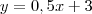
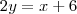




 .
.
 :
: