O meu problema aqui foi encontrar o fluxo do campo dado por
 ao redor de uma elipse dada por
ao redor de uma elipse dada por  , cujo intervalo de t varia de
, cujo intervalo de t varia de ![[0,2\pi] [0,2\pi]](/latexrender/pictures/1cc5fb6d3b10cf0b4029e23d46fa7fc0.png) .
.Na verdade o meu problema é que a minha resposta não está de acordo com o gabarito, já havia tentado passo a passo a achar os semi-eixos dessa elipse, até provei a área de uma elipse que é
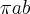 utilizando mesmo o próprio Teorema de Green. Então, usei a função paramétrica e eliminei o parâmetro para achar a equação cartesiana dessa elipse parametrizada, que deu
utilizando mesmo o próprio Teorema de Green. Então, usei a função paramétrica e eliminei o parâmetro para achar a equação cartesiana dessa elipse parametrizada, que deu 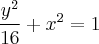 , cujo semi-eixo maior é 4 e semi-eixo menor é 1. Então, o fluxo que eu achei foi
, cujo semi-eixo maior é 4 e semi-eixo menor é 1. Então, o fluxo que eu achei foi 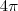 , mas o gabarito deu
, mas o gabarito deu  . Então, o que pode ter errado nessa questão? Se alguém puder esclarecer, eu agradeço.
. Então, o que pode ter errado nessa questão? Se alguém puder esclarecer, eu agradeço.Grato.







 ao redor e através da elipse que eu citei no post. Já que eu consegui transformar a equação parametrizada numa equação normal, já dá para fazer integral.
ao redor e através da elipse que eu citei no post. Já que eu consegui transformar a equação parametrizada numa equação normal, já dá para fazer integral.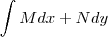 . Só que no caso da elipse, a soma das derivadas tem que dar 1, aí o que eu fiz: Eu chamei N de X e M também X, pois se eu considerar como uma integral dupla, o somatório das derivadas realmente dá 1. Só que eu não quis deixar na forma de integral dupla para não dar muito trabalho na hora dos cálculos, mas a ideia minha é chamar M e N de x.
. Só que no caso da elipse, a soma das derivadas tem que dar 1, aí o que eu fiz: Eu chamei N de X e M também X, pois se eu considerar como uma integral dupla, o somatório das derivadas realmente dá 1. Só que eu não quis deixar na forma de integral dupla para não dar muito trabalho na hora dos cálculos, mas a ideia minha é chamar M e N de x.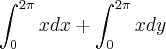 Convertendo tudo para coordenadas polares, ficou assim:
Convertendo tudo para coordenadas polares, ficou assim: =
= ![-16\int_{0}^{2\pi}sen\theta cos\theta d\theta + 2 \int_{0}^{2\pi}[1+cos(2\theta)] d\theta -16\int_{0}^{2\pi}sen\theta cos\theta d\theta + 2 \int_{0}^{2\pi}[1+cos(2\theta)] d\theta](/latexrender/pictures/602f0b2988fa5ffbff5033cd2562c6f1.png) =
= 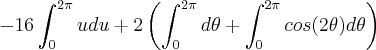 =
=  .
.
 .
.



