 por carlospires78 » Ter Out 27, 2009 09:19
por carlospires78 » Ter Out 27, 2009 09:19
seja f uma função real

x


:f(x+a)=1/2+
![\sqrt[]{} \sqrt[]{}](/latexrender/pictures/fe30ef6b9007d97ba11036078c300fe0.png)
f(x)-[f(x)]².F é periódica? justifique.
SEQUINDO O ENUNCIADO USEI O CONCEITO DE FUNÇÃO PERIÓDICA F(x+a)=f(x) , mas não consigo mostrar que ela é periódica .
-
carlospires78
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Out 27, 2009 08:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por BlackFoxes » Sáb Dez 26, 2009 05:08
por BlackFoxes » Sáb Dez 26, 2009 05:08
Olá. Também raciocinei assim. Se
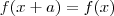
para todo x, então f é periódica. Basta provar que a igualdade é verdadeira ou não.
Logo:
![f(x)=\frac{1}{2}+\sqrt[2]{f(x)-{f(x)}^{2}} f(x)=\frac{1}{2}+\sqrt[2]{f(x)-{f(x)}^{2}}](/latexrender/pictures/3aa9bf0f7b46ff67f1843acca956b88f.png)



Ok, a função constante é periódica. Porém eu fiquei um pouco confuso, pois f é apenas períodica se f(x) assume os valores encontrados, porém
não necessariamente o faz.Espero que tenha ajudado em alguma coisa.
Abraços
-
BlackFoxes
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Dez 26, 2009 04:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dízimas Periódicas - Indução
por m0x0 » Seg Set 12, 2011 17:10
- 0 Respostas
- 823 Exibições
- Última mensagem por m0x0

Seg Set 12, 2011 17:10
Álgebra Elementar
-
- Encontre a fração geratriz da seguintes dizimas periódicas
por andersontricordiano » Sáb Abr 16, 2011 15:46
- 1 Respostas
- 2830 Exibições
- Última mensagem por Abelardo

Sáb Abr 16, 2011 16:23
Progressões
-
- exercicio resolv.funçoes
por adauto martins » Qui Ago 16, 2018 19:29
- 1 Respostas
- 3403 Exibições
- Última mensagem por adauto martins

Qui Ago 16, 2018 19:54
Funções
-
- exercicio resolv.funçoes
por adauto martins » Qua Jun 13, 2018 13:16
- 2 Respostas
- 4176 Exibições
- Última mensagem por adauto martins

Sex Jun 15, 2018 17:03
Funções
-
- exercicio resolv.-funçoes
por adauto martins » Ter Jul 31, 2018 20:41
- 1 Respostas
- 3070 Exibições
- Última mensagem por adauto martins

Ter Jul 31, 2018 21:14
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 x
x
 :f(x+a)=1/2+
:f(x+a)=1/2+![\sqrt[]{} \sqrt[]{}](/latexrender/pictures/fe30ef6b9007d97ba11036078c300fe0.png) f(x)-[f(x)]².F é periódica? justifique.
f(x)-[f(x)]².F é periódica? justifique.
 x
x
 :f(x+a)=1/2+
:f(x+a)=1/2+![\sqrt[]{} \sqrt[]{}](/latexrender/pictures/fe30ef6b9007d97ba11036078c300fe0.png) f(x)-[f(x)]².F é periódica? justifique.
f(x)-[f(x)]².F é periódica? justifique.
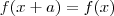 para todo x, então f é periódica. Basta provar que a igualdade é verdadeira ou não.
para todo x, então f é periódica. Basta provar que a igualdade é verdadeira ou não.![f(x)=\frac{1}{2}+\sqrt[2]{f(x)-{f(x)}^{2}} f(x)=\frac{1}{2}+\sqrt[2]{f(x)-{f(x)}^{2}}](/latexrender/pictures/3aa9bf0f7b46ff67f1843acca956b88f.png)




 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
