x
:f(x+a)=1/2+![\sqrt[]{}](/latexrender/pictures/fe30ef6b9007d97ba11036078c300fe0.png "\sqrt[]{}")
f(x)-[f(x)]².F é periódica? justifique.SEQUINDO O ENUNCIADO USEI O CONCEITO DE FUNÇÃO PERIÓDICA F(x+a)=f(x) , mas não consigo mostrar que ela é periódica .
por carlospires78 » Ter Out 27, 2009 09:19
x:f(x+a)=1/2+f(x)-[f(x)]².F é periódica? justifique.
por BlackFoxes » Sáb Dez 26, 2009 05:08
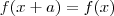para todo x, então f é periódica. Basta provar que a igualdade é verdadeira ou não.![f(x)=\frac{1}{2}+\sqrt[2]{f(x)-{f(x)}^{2}}](/latexrender/pictures/3aa9bf0f7b46ff67f1843acca956b88f.png "f(x)=\frac{1}{2}+\sqrt[2]{f(x)-{f(x)}^{2}}")
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)