O grafico da funçao f é o segmento de reta que une os pontos (22,2) e (2,0). O valor de f (1/2) é:
a) 1 b) 3/4 c)1/2 d) 1/8 e)7/8
A resposta dessa questã é a letra B, eu sei que é essa resposta mas não sei como realizar a equaçao que a define. Tente pelo y2-y1/x2-x1 e não consegui, então pesquisei e vi que no lugar de (22,2) é (-2,2), tentei do mesmo jeito e não consegui, me ajudem preciso da justificativa :'(


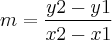

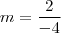
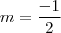
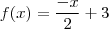
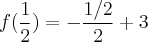
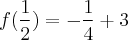
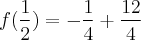
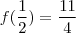



 .
.
 :
: