 por IlgssonBraga » Sáb Jul 26, 2014 15:30
por IlgssonBraga » Sáb Jul 26, 2014 15:30
Sejam
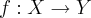
e
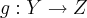
funções. Demonstre que:
Se gof é injetora e f é sobrejetora, então g é injetora. Onde gof=g(f(x)).
-
IlgssonBraga
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Jul 18, 2013 10:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
 por ant_dii » Sáb Jul 26, 2014 16:32
por ant_dii » Sáb Jul 26, 2014 16:32
Por definição, como

é sobrejetora, para qualquer
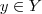
existe, pelo menos, um

tal que

.
Também por definição, como

é injetora segue que para
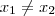
em

implica que
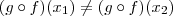
em

.
Mas

e

para
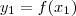
e
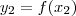
.
Logo,
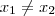
em

implica que

em

, ou seja,

é injetora. Note que

"cobre" todos os elementos de

, por ser sobrejetora ,portanto a implicação acima vale para qualquer elemento de

.
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por IlgssonBraga » Sáb Jul 26, 2014 16:42
por IlgssonBraga » Sáb Jul 26, 2014 16:42
Muito obrigado !!!
-
IlgssonBraga
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Jul 18, 2013 10:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função - Como proceder nesse caso?
por micheel » Dom Ago 18, 2013 22:37
- 1 Respostas
- 1993 Exibições
- Última mensagem por Russman

Dom Ago 18, 2013 23:16
Funções
-
- Como proceder... estou com duvidas...
por Netolucena » Dom Mar 18, 2012 18:32
- 2 Respostas
- 1663 Exibições
- Última mensagem por Netolucena

Dom Mar 18, 2012 22:06
Cálculo: Limites, Derivadas e Integrais
-
- analise real como proceder
por caciano-death » Sex Ago 25, 2017 17:56
- 2 Respostas
- 2127 Exibições
- Última mensagem por adauto martins

Qua Ago 30, 2017 11:36
Cálculo: Limites, Derivadas e Integrais
-
- Como resolvo problemas desse tipo?
por PriscilaMG » Dom Nov 22, 2009 12:25
- 1 Respostas
- 1898 Exibições
- Última mensagem por PriscilaMG

Dom Nov 22, 2009 12:33
Logaritmos
-
- como resolver esse tipo de conta?
por LuizCarlos » Seg Jul 11, 2011 00:43
- 11 Respostas
- 6170 Exibições
- Última mensagem por LuizCarlos

Ter Jul 12, 2011 20:00
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
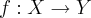 e
e 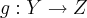 funções. Demonstre que:
funções. Demonstre que:
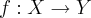 e
e 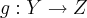 funções. Demonstre que:
funções. Demonstre que:
 é sobrejetora, para qualquer
é sobrejetora, para qualquer 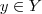 existe, pelo menos, um
existe, pelo menos, um  tal que
tal que  .
. é injetora segue que para
é injetora segue que para 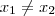 em
em  implica que
implica que 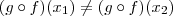 em
em  .
. e
e  para
para 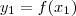 e
e 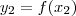 .
.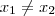 em
em  implica que
implica que  em
em  , ou seja,
, ou seja,  é injetora. Note que
é injetora. Note que  "cobre" todos os elementos de
"cobre" todos os elementos de  , por ser sobrejetora ,portanto a implicação acima vale para qualquer elemento de
, por ser sobrejetora ,portanto a implicação acima vale para qualquer elemento de  .
.


 .
.



