 por DanielFerreira » Dom Jul 20, 2014 13:15
por DanielFerreira » Dom Jul 20, 2014 13:15
Olá fff,
boa tarde!
Sabemos que

;
Façamos
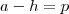
por conseguinte
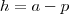
, então:

"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por e8group » Dom Jul 20, 2014 16:14
por e8group » Dom Jul 20, 2014 16:14
Boa tarde a todos ...
Alternativamente , fixado

, defina

. Dizer que

equivale dizer que para qualquer

dado , existe

(correspondente ) tal que se

então
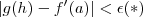
.
Segue que
![\frac{f(a+h) -f(a-h) }{2h} -f'(a) = \frac{f(a+h) -f(a) -(f(a-h) -f(a)) }{2h} -f'(a) = g(h) - \frac{f(a +(-h) ) -f(a)}{2h} -f'(a) = \frac{1}{2} \left[ g(h) - f'(a) - g(-h) - f'(a) \right] \frac{f(a+h) -f(a-h) }{2h} -f'(a) = \frac{f(a+h) -f(a) -(f(a-h) -f(a)) }{2h} -f'(a) = g(h) - \frac{f(a +(-h) ) -f(a)}{2h} -f'(a) = \frac{1}{2} \left[ g(h) - f'(a) - g(-h) - f'(a) \right]](/latexrender/pictures/b84640858021fb205aac98b2736dbc3d.png)
.
. Aplicando o módulo e usando a desigualdade triangular , temos

.
Mas , se

então
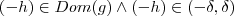
. Desta forma , obtemos que ambas quantidades

e

são limitadas por

e por isso

o que prova formalmente que o limite

existe e vale

.
Viva a matemática ...
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivada num ponto pela definição
por emsbp » Sex Jul 13, 2012 16:52
- 1 Respostas
- 1571 Exibições
- Última mensagem por Russman

Sex Jul 13, 2012 18:09
Cálculo: Limites, Derivadas e Integrais
-
- [derivada] derivada pela definição da secante
por TheKyabu » Sáb Out 27, 2012 23:24
- 2 Respostas
- 10879 Exibições
- Última mensagem por TheKyabu

Dom Out 28, 2012 11:44
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] DERIVADA POR DEFINIÇÃO DA RAIZ DO MÓDULO DE X
por Matheusgdp » Qua Set 16, 2015 04:07
- 2 Respostas
- 5107 Exibições
- Última mensagem por Matheusgdp

Qui Set 17, 2015 18:31
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] Duvida em derivada da definição.
por paulohenrique_ » Dom Dez 09, 2012 16:05
- 1 Respostas
- 1928 Exibições
- Última mensagem por young_jedi

Dom Dez 09, 2012 18:12
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Derivada por definição
por temujin » Qui Mai 16, 2013 13:07
- 4 Respostas
- 2527 Exibições
- Última mensagem por Man Utd

Sex Mai 17, 2013 18:50
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





 ;
;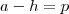 por conseguinte
por conseguinte 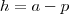 , então:
, então:

 , defina
, defina  . Dizer que
. Dizer que  equivale dizer que para qualquer
equivale dizer que para qualquer  dado , existe
dado , existe  (correspondente ) tal que se
(correspondente ) tal que se  então
então 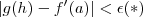 .
. ![\frac{f(a+h) -f(a-h) }{2h} -f'(a) = \frac{f(a+h) -f(a) -(f(a-h) -f(a)) }{2h} -f'(a) = g(h) - \frac{f(a +(-h) ) -f(a)}{2h} -f'(a) = \frac{1}{2} \left[ g(h) - f'(a) - g(-h) - f'(a) \right] \frac{f(a+h) -f(a-h) }{2h} -f'(a) = \frac{f(a+h) -f(a) -(f(a-h) -f(a)) }{2h} -f'(a) = g(h) - \frac{f(a +(-h) ) -f(a)}{2h} -f'(a) = \frac{1}{2} \left[ g(h) - f'(a) - g(-h) - f'(a) \right]](/latexrender/pictures/b84640858021fb205aac98b2736dbc3d.png) .
. .
.  então
então 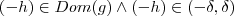 . Desta forma , obtemos que ambas quantidades
. Desta forma , obtemos que ambas quantidades  e
e  são limitadas por
são limitadas por  e por isso
e por isso  o que prova formalmente que o limite
o que prova formalmente que o limite  existe e vale
existe e vale  .
. 

 .
.



