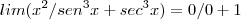
esse limite é quando x tende a zero pela direita 0+
assim eu poderia aplicar hopital só em
 ? e depois de achado o valor somar com lim sec^3x?
? e depois de achado o valor somar com lim sec^3x?
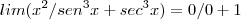
 ? e depois de achado o valor somar com lim sec^3x?
? e depois de achado o valor somar com lim sec^3x?
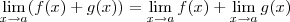 . (Exceto se é fácil ver que os limites existem ) , proceda assim ...
. (Exceto se é fácil ver que os limites existem ) , proceda assim ... 
 .
. 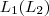 então pela regra operacional temos
então pela regra operacional temos 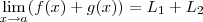 .
.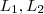 são números reais , entretanto suponha que um deles sejam não números reais e sim
são números reais , entretanto suponha que um deles sejam não números reais e sim  então
então  . Além disso , se ambos
. Além disso , se ambos 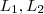 forem
forem  e
e 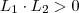 então
então  é possível mostrar isto formalmente . A teoria aq não está mt boa , recomendo que consulte livros .
é possível mostrar isto formalmente . A teoria aq não está mt boa , recomendo que consulte livros .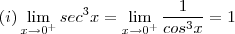 ( o limite lateral existe )
( o limite lateral existe )  (Não importa o " caminho " que seguirmos para computar o limite , importante é computar-ló corretamente )
(Não importa o " caminho " que seguirmos para computar o limite , importante é computar-ló corretamente )  .
. 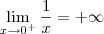 e
e  , logo
, logo 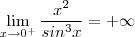 .
. sempre que
sempre que 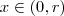 (para algum r > 0 pequeno fixado ) isto nos leva a concluir que
(para algum r > 0 pequeno fixado ) isto nos leva a concluir que 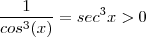 e com isso ganhamos a desigualdade (claramente verdadeira )
e com isso ganhamos a desigualdade (claramente verdadeira ) 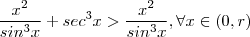 .
.  quando
quando 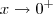 , ou seja
, ou seja  e o resultado segue .
e o resultado segue .

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
zig escreveu:

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.