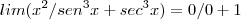
esse limite é quando x tende a zero pela direita 0+
assim eu poderia aplicar hopital só em
 ? e depois de achado o valor somar com lim sec^3x?
? e depois de achado o valor somar com lim sec^3x?
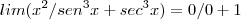
 ? e depois de achado o valor somar com lim sec^3x?
? e depois de achado o valor somar com lim sec^3x?
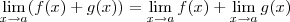 . (Exceto se é fácil ver que os limites existem ) , proceda assim ...
. (Exceto se é fácil ver que os limites existem ) , proceda assim ... 
 .
. 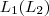 então pela regra operacional temos
então pela regra operacional temos 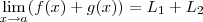 .
.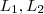 são números reais , entretanto suponha que um deles sejam não números reais e sim
são números reais , entretanto suponha que um deles sejam não números reais e sim  então
então  . Além disso , se ambos
. Além disso , se ambos 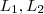 forem
forem  e
e 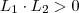 então
então  é possível mostrar isto formalmente . A teoria aq não está mt boa , recomendo que consulte livros .
é possível mostrar isto formalmente . A teoria aq não está mt boa , recomendo que consulte livros .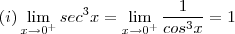 ( o limite lateral existe )
( o limite lateral existe )  (Não importa o " caminho " que seguirmos para computar o limite , importante é computar-ló corretamente )
(Não importa o " caminho " que seguirmos para computar o limite , importante é computar-ló corretamente )  .
. 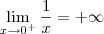 e
e  , logo
, logo 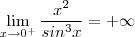 .
. sempre que
sempre que 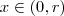 (para algum r > 0 pequeno fixado ) isto nos leva a concluir que
(para algum r > 0 pequeno fixado ) isto nos leva a concluir que 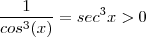 e com isso ganhamos a desigualdade (claramente verdadeira )
e com isso ganhamos a desigualdade (claramente verdadeira ) 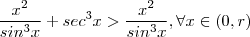 .
.  quando
quando 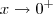 , ou seja
, ou seja  e o resultado segue .
e o resultado segue .

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.