 por ulisses123 » Sex Jun 20, 2014 15:23
por ulisses123 » Sex Jun 20, 2014 15:23
A sucessão (Zn ) é definida por Zn =(-1)^n/3n + (-1)^n-1
24.1 Calcule a somados seus quatro primeiros termos.
24.2 Prove que (Zn )é limitada.
24.3 Prove que (Zn ) não é convergente
-
ulisses123
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Sex Jun 20, 2014 14:48
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: curso tecnico em gestao
- Andamento: formado
 por e8group » Sex Jun 20, 2014 15:48
por e8group » Sex Jun 20, 2014 15:48
No primeiro não há muito o que fazer ; só computar
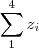
. No segundo , tome módulo e use desigualdade triangular para obter

. Para o último, sugiro que trabalhe com as duas sub-sequências

e

, oque se pode dizer sobre seus limites ??
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por ulisses123 » Dom Jun 29, 2014 14:34
por ulisses123 » Dom Jun 29, 2014 14:34
olá, eu não sei o que são subsucessoes,nem entendi acerca da desigualdade triangular,pode me ajudar por favor
-
ulisses123
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Sex Jun 20, 2014 14:48
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: curso tecnico em gestao
- Andamento: formado
 por e8group » Dom Jun 29, 2014 16:25
por e8group » Dom Jun 29, 2014 16:25
(I) Desigualdade triangular :
Na geometria Euclidiana , o comprimento de um lado de um triângulo é sempre menor que a soma dos demais comprimentos .Em analogia , tem-se que
dados

reais quaisquer , vale a desigualdade
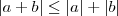
.
(II) Dada uma sequência (ou sucessão)

( ou apenas denotando
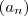
) .Uma subsequencia desta sequência, a grosso modo é uma nova sequência com termos da primeira sequência e estes termos respeita a ordenação da sequência original .
Ex.:
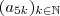
é uma subsequência de
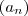
(iii) Uma sequência
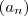
é limitada se existe

tal que
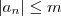
(

) .
A distância de

à origem (0 ) nunca será superior a

.
Para resolver o exercício . Tome

e

. Aplique a desigualdade e determine algum

. (Isto provará que ela é limitada)
E calcule os limites das duas subsequências de termos com índice par e impar ; mostre que os limites diferem o que equivale dizer que sequência não converge .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por ulisses123 » Dom Jul 06, 2014 12:10
por ulisses123 » Dom Jul 06, 2014 12:10
olá, santiago por favor, resolva esses dois itens: provar que se ela é limitada, e que não estou a conseguir fazer
-
ulisses123
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Sex Jun 20, 2014 14:48
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: curso tecnico em gestao
- Andamento: formado
 por e8group » Dom Jul 06, 2014 13:23
por e8group » Dom Jul 06, 2014 13:23
Note que ,
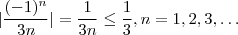
e

.
Segue-se que
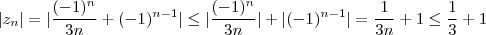
, para todo
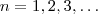
o que prova que

é limitada .
Quanto a divergência da sequência , basta notar que computando o limite da subsequencia

vamos obter

.
Por outro lado , computando o limite da outra subsequência

teremos

(verifique !)
Hipótese

tese (Se uma sequência converge , então toda subsequência converge para o mesmo limite )
Negação da tese

negação da hipótese ( existe duas subsequências distintas 'convergindo' para limites distintos o que implica que a sequência não converge )
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por ulisses123 » Dom Jul 06, 2014 15:26
por ulisses123 » Dom Jul 06, 2014 15:26
olá,santiago muito obrigado, somente por favor me ajuda nessa: sendo Un=n-(-1)^n, como provar que ela é não limitada,
-
ulisses123
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Sex Jun 20, 2014 14:48
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: curso tecnico em gestao
- Andamento: formado
 por e8group » Dom Jul 06, 2014 16:11
por e8group » Dom Jul 06, 2014 16:11
Ok , Mas ,na próxima vez utilize o sistema LaTeX e crie um novo tópico para um novo exercício .
Proposta 1 ( Prova por contradição )
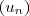
é limitada se é limitada inferiormente e superiormente .
Suponha (por absurdo )
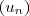
limitada e portanto
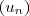
limitada superiormente .
Seja

uma cota superior a qual cumpre com

para todo

natural .
Tome qualquer
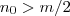
natural ( propriedade arquimediana assegura a des.) . Note que ,
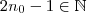
e

que contradiz a suposição .
Portanto

não é limitada superiormente o que implica que não é limitada .
Proposta 2 :
Pela desigualdade triangular
![n= |n| = | [n -(-1)^n ] + (-1)^n| \leq |u_n| + |(-1)^n| = |u_n| + 1 n= |n| = | [n -(-1)^n ] + (-1)^n| \leq |u_n| + |(-1)^n| = |u_n| + 1](/latexrender/pictures/d76365adffa16ea2994f60fc8adfe743.png)
e portanto
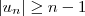
. Passando ao limite com

e notando que

o resultado segue .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Sequências
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- sucessões
por joanafrancisca » Ter Jul 24, 2012 23:23
- 2 Respostas
- 2269 Exibições
- Última mensagem por joanafrancisca

Qua Jul 25, 2012 01:53
Cálculo: Limites, Derivadas e Integrais
-
- Limities sucessões
por matpet92 » Qui Fev 02, 2012 22:13
- 4 Respostas
- 3669 Exibições
- Última mensagem por matpet92

Dom Fev 05, 2012 20:29
Cálculo: Limites, Derivadas e Integrais
-
- Limites de Funções vs Sucessões
por joaofonseca » Seg Mai 02, 2011 22:56
- 1 Respostas
- 2353 Exibições
- Última mensagem por LuizAquino

Seg Mai 02, 2011 23:09
Cálculo: Limites, Derivadas e Integrais
-
- Limite em sucessões - Cálculo
 por EREGON » Seg Nov 10, 2014 21:02
por EREGON » Seg Nov 10, 2014 21:02
- 6 Respostas
- 7812 Exibições
- Última mensagem por adauto martins

Qui Nov 13, 2014 14:27
Cálculo: Limites, Derivadas e Integrais
-
- Conclusão sobre Limite de sucessões
 por EREGON » Sex Nov 14, 2014 15:00
por EREGON » Sex Nov 14, 2014 15:00
- 2 Respostas
- 3912 Exibições
- Última mensagem por EREGON

Seg Nov 17, 2014 13:19
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



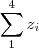 . No segundo , tome módulo e use desigualdade triangular para obter
. No segundo , tome módulo e use desigualdade triangular para obter  . Para o último, sugiro que trabalhe com as duas sub-sequências
. Para o último, sugiro que trabalhe com as duas sub-sequências  e
e  , oque se pode dizer sobre seus limites ??
, oque se pode dizer sobre seus limites ??

 reais quaisquer , vale a desigualdade
reais quaisquer , vale a desigualdade 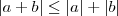 .
.  ( ou apenas denotando
( ou apenas denotando 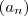 ) .Uma subsequencia desta sequência, a grosso modo é uma nova sequência com termos da primeira sequência e estes termos respeita a ordenação da sequência original .
) .Uma subsequencia desta sequência, a grosso modo é uma nova sequência com termos da primeira sequência e estes termos respeita a ordenação da sequência original . 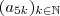 é uma subsequência de
é uma subsequência de 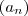
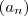 é limitada se existe
é limitada se existe  tal que
tal que 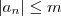 (
( ) .
) . à origem (0 ) nunca será superior a
à origem (0 ) nunca será superior a  .
. e
e  . Aplique a desigualdade e determine algum
. Aplique a desigualdade e determine algum  . (Isto provará que ela é limitada)
. (Isto provará que ela é limitada) 

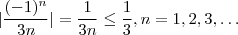 e
e  .
. 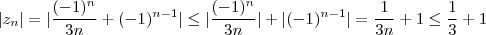 , para todo
, para todo 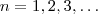 o que prova que
o que prova que  é limitada .
é limitada .  vamos obter
vamos obter  .
.  teremos
teremos  (verifique !)
(verifique !)  tese (Se uma sequência converge , então toda subsequência converge para o mesmo limite )
tese (Se uma sequência converge , então toda subsequência converge para o mesmo limite )  negação da hipótese ( existe duas subsequências distintas 'convergindo' para limites distintos o que implica que a sequência não converge )
negação da hipótese ( existe duas subsequências distintas 'convergindo' para limites distintos o que implica que a sequência não converge )

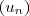 é limitada se é limitada inferiormente e superiormente .
é limitada se é limitada inferiormente e superiormente . 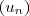 limitada e portanto
limitada e portanto 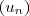 limitada superiormente .
limitada superiormente .  uma cota superior a qual cumpre com
uma cota superior a qual cumpre com  para todo
para todo  natural .
natural . 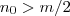 natural ( propriedade arquimediana assegura a des.) . Note que ,
natural ( propriedade arquimediana assegura a des.) . Note que , 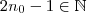 e
e  que contradiz a suposição .
que contradiz a suposição .  não é limitada superiormente o que implica que não é limitada .
não é limitada superiormente o que implica que não é limitada .![n= |n| = | [n -(-1)^n ] + (-1)^n| \leq |u_n| + |(-1)^n| = |u_n| + 1 n= |n| = | [n -(-1)^n ] + (-1)^n| \leq |u_n| + |(-1)^n| = |u_n| + 1](/latexrender/pictures/d76365adffa16ea2994f60fc8adfe743.png) e portanto
e portanto 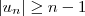 . Passando ao limite com
. Passando ao limite com  e notando que
e notando que  o resultado segue .
o resultado segue .


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.