A sucessão (Zn ) é definida por Zn =(-1)^n/3n + (-1)^n-1
24.1 Calcule a somados seus quatro primeiros termos.
24.2 Prove que (Zn )é limitada.
24.3 Prove que (Zn ) não é convergente



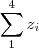 . No segundo , tome módulo e use desigualdade triangular para obter
. No segundo , tome módulo e use desigualdade triangular para obter  . Para o último, sugiro que trabalhe com as duas sub-sequências
. Para o último, sugiro que trabalhe com as duas sub-sequências  e
e  , oque se pode dizer sobre seus limites ??
, oque se pode dizer sobre seus limites ??

 reais quaisquer , vale a desigualdade
reais quaisquer , vale a desigualdade 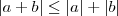 .
.  ( ou apenas denotando
( ou apenas denotando 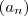 ) .Uma subsequencia desta sequência, a grosso modo é uma nova sequência com termos da primeira sequência e estes termos respeita a ordenação da sequência original .
) .Uma subsequencia desta sequência, a grosso modo é uma nova sequência com termos da primeira sequência e estes termos respeita a ordenação da sequência original . 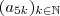 é uma subsequência de
é uma subsequência de 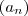
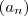 é limitada se existe
é limitada se existe  tal que
tal que 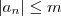 (
( ) .
) . à origem (0 ) nunca será superior a
à origem (0 ) nunca será superior a  .
. e
e  . Aplique a desigualdade e determine algum
. Aplique a desigualdade e determine algum  . (Isto provará que ela é limitada)
. (Isto provará que ela é limitada) 

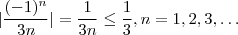 e
e  .
. 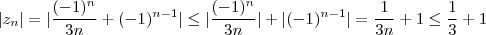 , para todo
, para todo 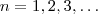 o que prova que
o que prova que  é limitada .
é limitada .  vamos obter
vamos obter  .
.  teremos
teremos  (verifique !)
(verifique !)  tese (Se uma sequência converge , então toda subsequência converge para o mesmo limite )
tese (Se uma sequência converge , então toda subsequência converge para o mesmo limite )  negação da hipótese ( existe duas subsequências distintas 'convergindo' para limites distintos o que implica que a sequência não converge )
negação da hipótese ( existe duas subsequências distintas 'convergindo' para limites distintos o que implica que a sequência não converge )

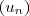 é limitada se é limitada inferiormente e superiormente .
é limitada se é limitada inferiormente e superiormente . 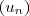 limitada e portanto
limitada e portanto 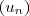 limitada superiormente .
limitada superiormente .  uma cota superior a qual cumpre com
uma cota superior a qual cumpre com  para todo
para todo  natural .
natural . 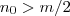 natural ( propriedade arquimediana assegura a des.) . Note que ,
natural ( propriedade arquimediana assegura a des.) . Note que , 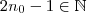 e
e  que contradiz a suposição .
que contradiz a suposição .  não é limitada superiormente o que implica que não é limitada .
não é limitada superiormente o que implica que não é limitada .![n= |n| = | [n -(-1)^n ] + (-1)^n| \leq |u_n| + |(-1)^n| = |u_n| + 1 n= |n| = | [n -(-1)^n ] + (-1)^n| \leq |u_n| + |(-1)^n| = |u_n| + 1](/latexrender/pictures/d76365adffa16ea2994f60fc8adfe743.png) e portanto
e portanto 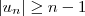 . Passando ao limite com
. Passando ao limite com  e notando que
e notando que  o resultado segue .
o resultado segue .
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes