no ponto p = (0,0)
Não estou conseguindo identificar se a função é ou não diferenciável.
Se não tiver compreendido a função, existe uma imagem em anexo abaixo.




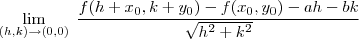 onde
onde  , e ,
, e ,  e este "limitão" obrigatoriamente deve ser zero para a função ser diferenciavel no ponto
e este "limitão" obrigatoriamente deve ser zero para a função ser diferenciavel no ponto 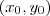 caso não seja feita esta condição a função não é diferenciavél em
caso não seja feita esta condição a função não é diferenciavél em 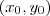 .
.


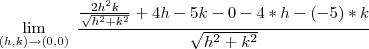

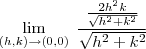
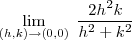
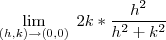
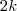 vai a zero quando
vai a zero quando  e que
e que 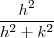 é limitada em
é limitada em ![\left[0,1 \right] \left[0,1 \right]](/latexrender/pictures/7677ea85fbaa1efa02fd80baa7e802de.png) , para provar isto faça :
, para provar isto faça :
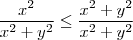

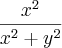 é sempre positivo , então o menor valor que pode assumir é quando
é sempre positivo , então o menor valor que pode assumir é quando que implica que
que implica que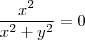 , daí obtemos que esta função é limitada e sua imagem é
, daí obtemos que esta função é limitada e sua imagem é ![\left[0,1 \right] \left[0,1 \right]](/latexrender/pictures/7677ea85fbaa1efa02fd80baa7e802de.png) .
. , então como o limite é zero segue que a função
, então como o limite é zero segue que a função  é diferenciavél no ponto
é diferenciavél no ponto 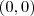 .
.

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes

 .
.
 :
: