 por Marcos07 » Seg Jun 30, 2014 14:42
por Marcos07 » Seg Jun 30, 2014 14:42
Compreendo exercícios que envolvam aplicação simples, mas estou tendo bastante dificuldade em definições desse gênero.
Ps: R^n significa R elevado a (n) enésima potência.
C significa está contido.
€ significa pertence
Editado pela última vez por
Marcos07 em Ter Jul 01, 2014 01:33, em um total de 1 vez.
-
Marcos07
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Seg Jun 30, 2014 01:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Ter Jul 01, 2014 00:59
por e8group » Ter Jul 01, 2014 00:59
As notações não ficaram 100 % claras , por favor sempre use o sist. LaTeX . Estou supondo que ,
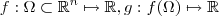
são as aplicações dadas . E desejamos mostrar que a composta

é contínua em

, certo ?
(Use as hipóteses )

é contínua em
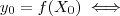

.

é contínua em
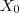
, então existe

t.q
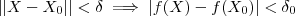
(mesmo delta_0 que utilizamos acima ) ; logo
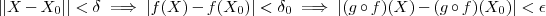
.
E ...
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Marcos07 » Ter Jul 01, 2014 01:21
por Marcos07 » Ter Jul 01, 2014 01:21
Muito obrigado mesmo. Muito claro e objetivo. nem sabe o quanto me ajudou. valeu mesmo!!!
-
Marcos07
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Seg Jun 30, 2014 01:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- calculo integral, funçoes continuas
por caciano-death » Qua Mai 18, 2016 10:26
- 2 Respostas
- 6771 Exibições
- Última mensagem por caciano-death

Qui Ago 25, 2016 10:39
Cálculo: Limites, Derivadas e Integrais
-
- Funções contínuas
por Rafinha_84 » Dom Fev 23, 2014 20:57
- 1 Respostas
- 1495 Exibições
- Última mensagem por Russman

Seg Fev 24, 2014 00:24
Funções
-
- Função contínuas com derivadas de todas as ordens contínuas
por Janoca » Dom Jun 15, 2014 20:40
- 2 Respostas
- 2242 Exibições
- Última mensagem por Janoca

Dom Jun 15, 2014 21:12
Cálculo: Limites, Derivadas e Integrais
-
- [Frações Contínuas] Número pi
por matheus_vitorf » Ter Jul 25, 2017 16:43
- 0 Respostas
- 2256 Exibições
- Última mensagem por matheus_vitorf

Ter Jul 25, 2017 16:43
Teoria dos Números
-
- varíaveis aleatórias contínuas conjuntas
por gprestes » Qua Nov 24, 2010 08:38
- 0 Respostas
- 2535 Exibições
- Última mensagem por gprestes

Qua Nov 24, 2010 08:38
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



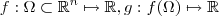 são as aplicações dadas . E desejamos mostrar que a composta
são as aplicações dadas . E desejamos mostrar que a composta  é contínua em
é contínua em  , certo ?
, certo ?  é contínua em
é contínua em 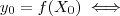
 .
.  é contínua em
é contínua em 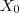 , então existe
, então existe  t.q
t.q 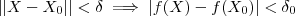 (mesmo delta_0 que utilizamos acima ) ; logo
(mesmo delta_0 que utilizamos acima ) ; logo 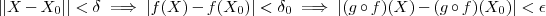 .
. 



 , avisa que eu resolvo.
, avisa que eu resolvo.

