[integral indefinida] - dúvida

por **natanaelskt** » Sáb Jun 28, 2014 09:25

estou com dúvida na resolução deste exercício de integral indefinia.caiu na minha prova e eu errei. na verdade,nem sei como começa.
obrigado desde já. postei a foto do exercício em anexo.

por **e8group** » Sáb Jun 28, 2014 14:13

Novamente friso para anexar imagens se for necessário .

Bem , o processo natural é integrar por partes sucessivas vezes . Derivando-se ln(x) e multiplicando por um monômio da forma x^n

reduzirá a potência deste termo .

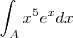Não gosto de fazer contas . Um certo dia precisei computar $\int_{A} x^5 e^x dx$ , entretanto percebi que

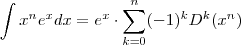$\int x^n e^x dx = e^x \cdot \sum_{k=0}^n (-1)^k D^k(x^n)$ . Onde o operador D^k

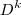a cada função k vezes diferenciável faz corresponde a

-ésima derivada da função , convencionado que D^0 (f(x)) =f(x)

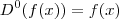. Pode-se provar a fórmula por indução .

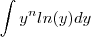Agora computaremos $\int y^n ln(y) dy$ . Duas substituições simples . Primeiro , deixe

$z = ln(y) \implies \begin{cases} dz = \frac{dy}{y} \end{cases} \\ y =e^z$ .

Assim ,

$\int y^n ln(y) dy = \int y^{n+1} \frac{ln(y)}{y} dy = \int (e^z)^{n+1} z dz = \int e^{(n+1)z} z dz$ .

Segundo , deixe (n+1)z = x

....

$\int e^{(n+1)z} z dz = ... = \frac{1}{(n+1)^2} \int x \cdot e^x dx$ .

Está última integral pode ser calculada por partes ... ou simplesmente aplicação da formula ,
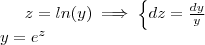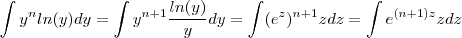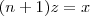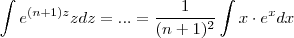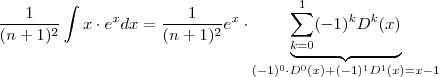$\frac{1}{(n+1)^2} \int x \cdot e^x dx = \frac{1}{(n+1)^2} e^x \cdot \underbrace{\sum_{k=0}^1 (-1)^k D^k(x) }_{(-1)^0 \cdot D^0(x) + (-1)^1 D^1(x) = x - 1 }$ , ou seja

$\frac{1}{(n+1)^2} \int x \cdot e^x dx = e^x (x-1) = \frac{1}{(n+1)^2} e^{(n+1)z}(-1+(n+1)z) = \frac{1}{(n+1)^2} e^{(n+1)ln(y)}(-1+(n+1)ln(y)) = \frac{1}{(n+1)^2} y^{n+1} (-1+ [n+1]ln(y) )$ , em particular com n = 3

terá o resultado .

por **natanaelskt** » Sáb Jun 28, 2014 16:28

muito obrigado sathiago. estou com dúvida em mais alguns exercícios. eu posso continuar postando em imagens? eu não sei utilizar o látex. já tentei,mas tô perdendo muito tempo e acaba saindo errado.
muito obrigado. me ajudou muito

por **e8group** » Sáb Jun 28, 2014 17:16

Não há de quê . Mais dúvidas compartilha com a comunidade .Como disse é uma das regras da casa deixar organizado o fórum . No inicio é difícil digitar as equações usando o LaTeX , e nesta fase recomendo o site http://www.codecogs.com/latex/eqneditor.php o qual contém uma tabela com os símbolos .Assim , por exemplo , clicando sobre o simbolo da integral , terá o código \int e a imagem compilada gerando tal simbolo . Mas , se não conseguir acredito que pode sim continuar a postar os exercícios como tem feito até você se adaptar com o LaTeX .Importante é não deixar dúvidas pendentes . E outro fator importante , tente expor o que você tentou , quais as dúvidas e etc .