Preciso calcular o terceiro lado de um triângulo, para encontrar seus ângulos internos que serão usados na decomposição vetorial de forças em um problema mecânico.
Desenhei o diagrama das medidas conhecidas e o valor que preciso (o x em vermelho).
Tentei por mais de uma hora e não consegui nada.. Alguém pode me dar uma força?

Obrigado!


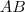 e
e  congruentes e base
congruentes e base  e
e 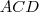 o triângulo de lados medindo
o triângulo de lados medindo ![\overline{AC} = x , \overline{AD} = 3 , \overline{AD}
Tome como verdade ( ou prove ) que [tex] \overline{AM} \overline{AC} = x , \overline{AD} = 3 , \overline{AD}
Tome como verdade ( ou prove ) que [tex] \overline{AM}](/latexrender/pictures/d6b1fb2aeb07389f9d09ec2804bf796d.png) é a altura do trapézio . Em seguida , tome
é a altura do trapézio . Em seguida , tome  a interseção da reta que contém a base maior do trapézio com à reta que passa por
a interseção da reta que contém a base maior do trapézio com à reta que passa por  e é paralela a reta que contém
e é paralela a reta que contém 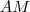 . Aceite (ou mostre) que
. Aceite (ou mostre) que 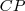 são congruentes e por conseguinte
são congruentes e por conseguinte 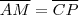 ,segue-se que
,segue-se que 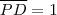 (Pq ?) .Como o triângulo PCD é T. retângulo , então pelo Teo. de Pitágoras ,
(Pq ?) .Como o triângulo PCD é T. retângulo , então pelo Teo. de Pitágoras , 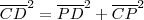 o que implica que
o que implica que 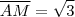 . Em seguida aplicando o Teo. de Pitágoras em
. Em seguida aplicando o Teo. de Pitágoras em 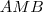 obterá
obterá  .
.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)