felipeek escreveu:Vamos supor que eu derive uma função F(x,y) parcialmente em relação a x, por exemplo, e obtenha uma nova função que dependa de ambos x e y. Neste caso, qual seria o sentido de y neste resultado? Seria y uma variável que simplesmente determina qual a "secção" que eu desejo "estudar", digamos assim? Por exemplo, ao tomar y=2, a função F'(x,2) mostraria a variação da variável x na secção de z e x com y fixado em 2. É por aí?
Exatamente. Por exemplo, considere a função
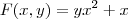
. Ao tomar a derivada parcial desta função com relação a x você obtém uma nova função
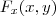
dada por
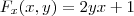
A função obtida é uma
família de funções lineares
em x, no sentido de que as inclinações são dependentes de y como facilmente se vê.
Note que se ao invés de trabalharmos com

variável e o substituíssemos por uma valor constante, por exemplo,

teríamos
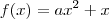
de onde
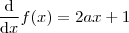
que exemplifica bem a tecnologia da derivação parcial.
felipeek escreveu:Outra pergunta, qual seria então o sentido da derivada total de F com relação a x?
A derivação total considera não só a dependência
explícita de uma certa variável na função de interesse como a
implícita. Suponha que você esteja estudando uma função
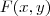
onde

. Ou seja, a variável

esta parametrizada. Desta forma a própria função F varia com o parâmetro

de modo que a derivada total calcula exatamente como se dá esta variação.
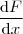 e
e 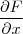
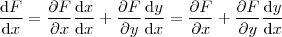
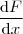 estamos levando em conta que y depende de x, ou algo do tipo. E quando fazemos
estamos levando em conta que y depende de x, ou algo do tipo. E quando fazemos 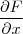 parece que y não depende de x ou que ignoramos este fato.
parece que y não depende de x ou que ignoramos este fato.



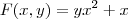 . Ao tomar a derivada parcial desta função com relação a x você obtém uma nova função
. Ao tomar a derivada parcial desta função com relação a x você obtém uma nova função 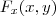 dada por
dada por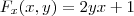
 variável e o substituíssemos por uma valor constante, por exemplo,
variável e o substituíssemos por uma valor constante, por exemplo,  teríamos
teríamos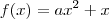
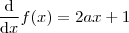
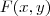 onde
onde  . Ou seja, a variável
. Ou seja, a variável  de modo que a derivada total calcula exatamente como se dá esta variação.
de modo que a derivada total calcula exatamente como se dá esta variação.
 , avisa que eu resolvo.
, avisa que eu resolvo.

