Ooops ! Na verdade não equivalente e sim uma implicação obvia . Já estudou G.A. ? Se sim , podemos interpretar qualquer sistema linear 2 por 2 como interseção entre duas retas , que em geral se exprimem por

. (a,b,c constantes com a ,b não simultaneamente nulas )
De forma geral , qualquer sistema linear m equações para n incógnitas pode ser visto como interseção entre

hiperplanos do

.
Por exemplo se m = 2 e n = 3 , o sistema de equações representa geometricamente uma reta no

(caso os planos não são paralelos ) .
Se quiser mais explicações com este foco , só dizer .
De forma sucinta ,

, corresponde a solução
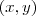
do sistema

.
Se você esboçar o gráfico de ambas retas verá que a interseção entre elas se resume a um ponto . Como queremos encontrar apenas y , basta multiplicar uma das equações por um número conveniente de modo que está equação multiplicada por este número somada a outra equação se resume apenas uma equação de uma variável y .
As contas deixo para você .


 , independente de
, independente de  ser discreto ou não , afirmamos que E é linear . Assim sendo , temos
ser discreto ou não , afirmamos que E é linear . Assim sendo , temos 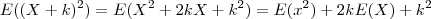 (1) .
(1) . 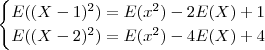 .
. , isso pq
, isso pq 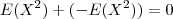 e qualquer solução da combinação linear não nula de
e qualquer solução da combinação linear não nula de  é também solução do sistema e a recíproca tbm é verdadeira .
é também solução do sistema e a recíproca tbm é verdadeira .
 . (a,b,c constantes com a ,b não simultaneamente nulas )
. (a,b,c constantes com a ,b não simultaneamente nulas )  hiperplanos do
hiperplanos do  .
.  (caso os planos não são paralelos ) .
(caso os planos não são paralelos ) . , corresponde a solução
, corresponde a solução 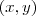 do sistema
do sistema  .
.