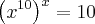
Tentei usar a propriedade de mudança de base e cheguei em
 mas não consegui sair daqui. Alguém poderia me ajudar?
mas não consegui sair daqui. Alguém poderia me ajudar?
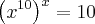
 mas não consegui sair daqui. Alguém poderia me ajudar?
mas não consegui sair daqui. Alguém poderia me ajudar?
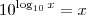 .
. e
e  são uma a inversa da outra. Isto é,
são uma a inversa da outra. Isto é,

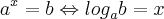
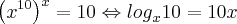
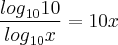 , e como log de 10 é 1 eu cheguei naquilo q te mandei.
, e como log de 10 é 1 eu cheguei naquilo q te mandei.
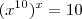 é uma equação? Isto é, você busca um valor
é uma equação? Isto é, você busca um valor  tal que
tal que 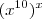 seja igual a
seja igual a  ? Veja que esta expressão não é uma identidade!!
? Veja que esta expressão não é uma identidade!!
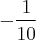 , mas não mostrou o processo de cálculo.
, mas não mostrou o processo de cálculo.
matheus_frs1 escreveu:Depois usei a mudança de base para chegar em , e como log de 10 é 1 eu cheguei naquilo q te mandei.
 )na equação. Assim, a expressão obtida é
)na equação. Assim, a expressão obtida é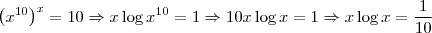
 possui a solução exata dada por
possui a solução exata dada por
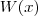 é a tal Função W de Lambert e
é a tal Função W de Lambert e  é o Número de Euler.
é o Número de Euler. . De fato, calculando
. De fato, calculando 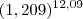 você obtém
você obtém 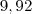 aproximadamente. Note que com 3 casas de precisão obtemos um erro +-0,07 no valor exato. Não é de todo mal.
aproximadamente. Note que com 3 casas de precisão obtemos um erro +-0,07 no valor exato. Não é de todo mal.


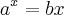 eu tenho que usar esse raciocínio?
eu tenho que usar esse raciocínio?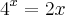 , tenho x no expoente do primeiro membro e x no segundo membro também. Se sim, gostaria de saber como devo proceder nesses tipos de exercícios, pq eu não entendi mto bem a resolução e também não encontrei vídeos a respeito.
, tenho x no expoente do primeiro membro e x no segundo membro também. Se sim, gostaria de saber como devo proceder nesses tipos de exercícios, pq eu não entendi mto bem a resolução e também não encontrei vídeos a respeito. 
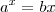 pode ser resolvida usando a Função W de Lambert.
pode ser resolvida usando a Função W de Lambert.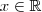 é tal que
é tal que ,
, 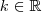
 .
.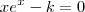 (1) então nossa esperança é que ao menos uma seja obtida pela função W de Lambert.
(1) então nossa esperança é que ao menos uma seja obtida pela função W de Lambert. para uma outra
para uma outra  . Mas antes, caso você não o conheça, vamos falar de
. Mas antes, caso você não o conheça, vamos falar de  .Este número
.Este número  é o chamado Número de Euler. É um número irracional. É com ele que se define a função exponencial
é o chamado Número de Euler. É um número irracional. É com ele que se define a função exponencial 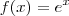 . Note que podemos usar esta função para escrever qualquer outra função de potência em qualquer outra base. Da definição de função logarítmica podemos escrever que
. Note que podemos usar esta função para escrever qualquer outra função de potência em qualquer outra base. Da definição de função logarítmica podemos escrever que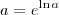
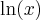 é a função logarítmica de base
é a função logarítmica de base  .
.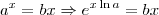 .
. e
e  vale
vale 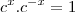 ? Então, vamos multiplicar a expressão obtida em ambos membros por
? Então, vamos multiplicar a expressão obtida em ambos membros por 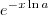 :
: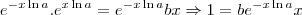
 . Veja
. Veja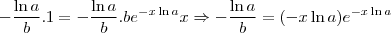
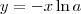 e
e  , então a equação acima se muda para
, então a equação acima se muda para
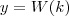
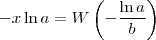
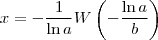
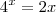 basta tomar,como eu imagino que você saiba,
basta tomar,como eu imagino que você saiba, 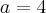 e
e  . Assim,
. Assim, 
 notamos que ela não possui solução Real. :(
notamos que ela não possui solução Real. :(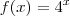 e sobreponha ao gráfico de
e sobreponha ao gráfico de 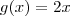 . Você verá que a função
. Você verá que a função 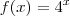 cresce muito rapidamente de modo que a função
cresce muito rapidamente de modo que a função 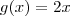 não a consegue alcançar em nenhum ponto
não a consegue alcançar em nenhum ponto  . Isto é, não existe
. Isto é, não existe 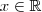 tal que
tal que  .
. . Repetindo o processo de graficar as funções nota-se facilmente que esta equação tem duas soluções
. Repetindo o processo de graficar as funções nota-se facilmente que esta equação tem duas soluções e
e  . É fácil de verificar. De fato,
. É fácil de verificar. De fato,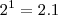

 .
. ou
ou  ou nenhum destes( no caso de termos azar). Da própria definição de função não pode existir dois valores para um mesmo
ou nenhum destes( no caso de termos azar). Da própria definição de função não pode existir dois valores para um mesmo  . Então a função W fornece ao menos uma raiz(ou nenhuma) da equação, como eu citei antes.
. Então a função W fornece ao menos uma raiz(ou nenhuma) da equação, como eu citei antes.


Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

