Em outras palavras , queremos verificar se estes pontos estão em um mesmo plano .Para tal , há mais de um método . Já aprendeu produto vetorial , interno ? Caso sim , uma forma é tomar o produto misto entre os três vetores construídos (usando todos os pontos dados ) e verificar o resultado. Caso não , veremos outra forma ...
Primeiro como definir a eq. de uma plano na forma paramétrica
Considere os pontos

(não colineares ) pertencendo a um plano
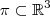
.
Podemos construir os vetores

e ambos são paralelos a

.
Agora seja

um ponto qualquer deste plano [/tex] . Construímos o vetor

, vemos que

se exprimir como soma de dois vetores , um paralelo a
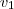
e o outro a
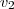
. Ou seja é ,

para

escalares .
Faça um esboço da situação descrita .
A relação acima nos permitir verificar se os pontos dados são coplanares .
Se o sistema

possui solução , então A,B,C,D estão em um mesmo plano . Caso contrário não .
Se você estudou também ,dependência, independência linear , de

, resulta que os vetores três vetores são L.D .
Outra forma seria verificar se os vetores são L.D. ou L.I. ...
Enfim , como disse mais de um método .
Se quiser ler mais , recomendo este material :
http://www.professores.uff.br/kowada/ga ... 1aula4.pdf


 (não colineares ) pertencendo a um plano
(não colineares ) pertencendo a um plano 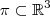 .
. e ambos são paralelos a
e ambos são paralelos a  .
.  um ponto qualquer deste plano [/tex] . Construímos o vetor
um ponto qualquer deste plano [/tex] . Construímos o vetor  , vemos que
, vemos que  se exprimir como soma de dois vetores , um paralelo a
se exprimir como soma de dois vetores , um paralelo a 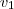 e o outro a
e o outro a 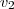 . Ou seja é ,
. Ou seja é , para
para  escalares .
escalares .  possui solução , então A,B,C,D estão em um mesmo plano . Caso contrário não .
possui solução , então A,B,C,D estão em um mesmo plano . Caso contrário não . , resulta que os vetores três vetores são L.D .
, resulta que os vetores três vetores são L.D . 
