


miguel135 escreveu:Quantas vezes em um dia um relógio normal (analógico) tem seus 3 ponteiros formando 120 graus entre si?


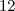 para
para  e o que indica minuto passar de
e o que indica minuto passar de  para
para  e o de segundo passar de
e o de segundo passar de 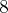 para
para 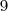 , teremos o segundo horário que o fato acontece que é às 01:25:45. E O processo continua ...
, teremos o segundo horário que o fato acontece que é às 01:25:45. E O processo continua ... 


miguel135 escreveu:santhiago, não é isso. Às 00:20:40 eles não formam 120 graus entre si(lembre-se que o ponteiro pequeno não está exatamente no "12" do relógio após 20min e 40s nem o o ponteiro do minuto esta exatamento no "4" do relógio).

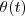 que cada ponteiro forma com um referencial fixo segue uma equação diferencial da forma
que cada ponteiro forma com um referencial fixo segue uma equação diferencial da forma  , onde
, onde  é uma constante. Ou seja, os ponteiros percorrem ângulos iguais em tempos iguais. Certo, isso não é novidade. Portanto se, por exemplo,
é uma constante. Ou seja, os ponteiros percorrem ângulos iguais em tempos iguais. Certo, isso não é novidade. Portanto se, por exemplo, 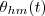 é o angulo formado entre o ponteiro dos minutos e das horas a cada instante te tempo, eu acredito que precisamos calcular um número
é o angulo formado entre o ponteiro dos minutos e das horas a cada instante te tempo, eu acredito que precisamos calcular um número  de vezes tal que
de vezes tal que 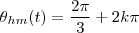 para o intervalo de tempo de 1 dia.
para o intervalo de tempo de 1 dia. ) todos os ponteiros formem com relação ao eixo vertical do relógio
) todos os ponteiros formem com relação ao eixo vertical do relógio 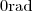 e o crescimento dos ângulos se dá no sentido horário. As velocidades angulares de cada ponteiro são para o das horas, minutos e segundos, respectivamente,
e o crescimento dos ângulos se dá no sentido horário. As velocidades angulares de cada ponteiro são para o das horas, minutos e segundos, respectivamente,  rad/s ,
rad/s ,  rad/2 e
rad/2 e  rad/s. Assim, as soluções das equações de crescimento são
rad/s. Assim, as soluções das equações de crescimento são


 . Daí, seguindo o raciocínio, precisamos calcular
. Daí, seguindo o raciocínio, precisamos calcular  tal que
tal que  para
para 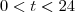 já que
já que  é à meia-noite. Fazendo a conta, encontramos que o menor
é à meia-noite. Fazendo a conta, encontramos que o menor  inteiro tal que
inteiro tal que  é
é  . Daí, o ângulo entre estes ponteiros será 120° 21 vezes por dia. (será q é certo isso ???)
. Daí, o ângulo entre estes ponteiros será 120° 21 vezes por dia. (será q é certo isso ???) fizesse o mesmo papel que
fizesse o mesmo papel que  no ângulo relativo entre o ponteiro dos minutos e segundos, por exemplo, eu acho que teríamos uma equação diofantina relacionando-os.
no ângulo relativo entre o ponteiro dos minutos e segundos, por exemplo, eu acho que teríamos uma equação diofantina relacionando-os.
 /6 rad/h
/6 rad/h /21.600)rad/s
/21.600)rad/s /1800)rad/s
/1800)rad/s /30)rad/s
/30)rad/s
 rad em 12h. Assim, sua velocidade é
rad em 12h. Assim, sua velocidade é  rad/h.
rad/h. rad a cada minuto. Como 1 minuto é
rad a cada minuto. Como 1 minuto é  de hora, então a velocidade será
de hora, então a velocidade será 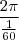 rad/h ou
rad/h ou  rad/h.
rad/h.





Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes