Bem, eu acredito que o "d" trate-se da razão da P.A..
Uma P.A. é uma sequência
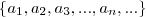
,finita ou infinita, que caracteriza-se pela relação:
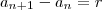
onde

é um numero real qualquer constante(isto é, independente n).
Resolve-se, para esta,

. Ainda, sabemos que a soma dos

primeiros termos da sequência, isto é,
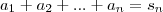
é tal que
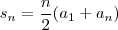
. Ou, de forma equivalente,
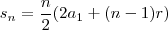
.
Assim, se a sua P.A. tem o termo
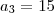
e
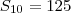
temos informações suficientes para determinar todos os seus termos.
Comece com a definição do termo geral:

. Daí, a primeira equação é esta.
Agora, do resultado para soma,
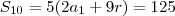
. Esta é a segunda equação.
Reunindo ambas, temos
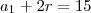
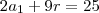
que é um sistema de equações de 1° grau 2x2. Resolva-o e terá o 1° termo da P.A. e a sua razão, de modo que , assim, será capaz de determinar qualquer um de seus termos.
Eu acredito que você deva calcular
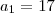
e
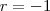
.



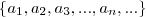 ,finita ou infinita, que caracteriza-se pela relação:
,finita ou infinita, que caracteriza-se pela relação: 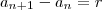 onde
onde  é um numero real qualquer constante(isto é, independente n).
é um numero real qualquer constante(isto é, independente n).  . Ainda, sabemos que a soma dos
. Ainda, sabemos que a soma dos  primeiros termos da sequência, isto é,
primeiros termos da sequência, isto é, 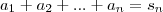 é tal que
é tal que 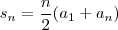 . Ou, de forma equivalente,
. Ou, de forma equivalente, 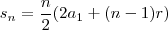 .
.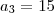 e
e 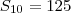 temos informações suficientes para determinar todos os seus termos.
temos informações suficientes para determinar todos os seus termos. . Daí, a primeira equação é esta.
. Daí, a primeira equação é esta.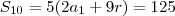 . Esta é a segunda equação.
. Esta é a segunda equação.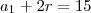
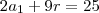
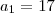 e
e 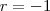 .
.
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.