Provar, pela definição, que
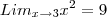
Para que isso seja verdade, por definição, deve
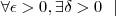
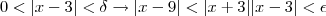
Vê-se que caso uma constante
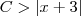 for encontrada, poderemos fazer
for encontrada, poderemos fazer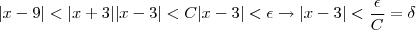 , de modo a conjecturar um valor para
, de modo a conjecturar um valor para 
Como queremos um
 pequeno, podemos supor que
pequeno, podemos supor que 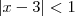 , e, através de algumas manipulações,
, e, através de algumas manipulações,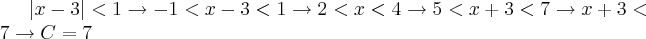
Portanto, encontramos um valor
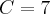 adequado; no entanto, adquirimos duas restrições para
adequado; no entanto, adquirimos duas restrições para 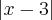 , quais sejam:
, quais sejam: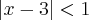 e
e 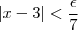
E, como
 , os dois valores sugestivamente parecem ser adequados para
, os dois valores sugestivamente parecem ser adequados para  ; assim, para satisfazer as duas equações, conjecturamos
; assim, para satisfazer as duas equações, conjecturamos ![\delta = min[{1, \dfrac{\epsilon}{7}] \delta = min[{1, \dfrac{\epsilon}{7}]](/latexrender/pictures/85f1f18e3890d11408745eebf5ce5ada.png) .
.Pois bem, no entanto, queremos a recíproca destas conclusões, analisamos-a:
Dado
 e
e ![\delta = min[{1, \dfrac{\epsilon}{7}] \delta = min[{1, \dfrac{\epsilon}{7}]](/latexrender/pictures/f2b83e9d3c07e78f23e5bf719bcee82d.png) , temos que:
, temos que:Se
 :
: 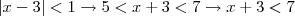
Se
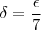 :
: 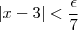
Nesse caso, vemos que:
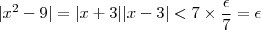
Assim, por definição, o limite sumariamente exposto é verdadeiro.
Agora vejamos para uma função do 3º grau:
Prove, pela definição, que
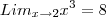
Isto é verdade, por definição, como anteriormente exposto, se, e somente se,
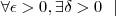
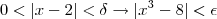
Vemos que |x^3 - 8| < |x-2||x^2+2x+4|, ou seja, se acharmos um
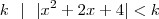 , poderemos fazer:
, poderemos fazer: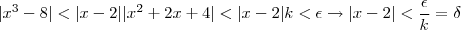
E a partir daí seguir como feito no exemplo anterior.
Eu gostaria de supor que
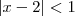 , mas não consegui isolar
, mas não consegui isolar 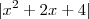 a partir daí... alguém pode me explicar como fazê-lo? Agradeço sugestões...
a partir daí... alguém pode me explicar como fazê-lo? Agradeço sugestões...

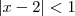 , obtemos:
, obtemos: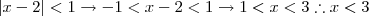 , daí:
, daí: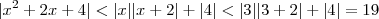
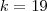 , certo?
, certo?
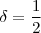 ou qualquer outro valor pequeno,Por exemplo :
ou qualquer outro valor pequeno,Por exemplo :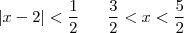
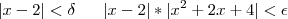
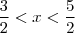 ,percebemos que :
,percebemos que : 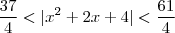 , então :
, então :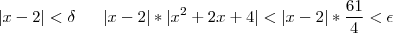
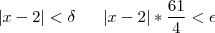
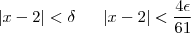
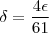 , então temos que :
, então temos que : ![\delta min=\left[\frac{1}{2},\frac{4 \epsilon}{61} \right] \delta min=\left[\frac{1}{2},\frac{4 \epsilon}{61} \right]](/latexrender/pictures/f2ce447e61c99bef3160531873009c3b.png) ,provando que funciona :
,provando que funciona :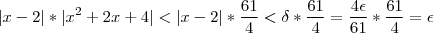

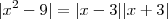 . Como estamos trabalhando com
. Como estamos trabalhando com  próximo de 3 , logo
próximo de 3 , logo 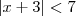 . E com isso ,
. E com isso , 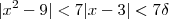 .Aqui já consigo ver que sua solução está coerente .
.Aqui já consigo ver que sua solução está coerente . 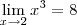 .
. 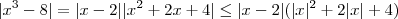 .
. 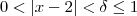 então
então 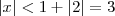 . Daí ,
. Daí , 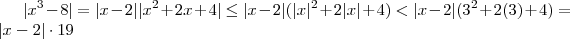 .
.  natural quaisquer , e para um ponto genérico
natural quaisquer , e para um ponto genérico  fixado e provar que
fixado e provar que 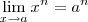 . O raciocínio é análogo para este caso mais geral .
. O raciocínio é análogo para este caso mais geral .