


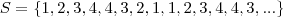 cujo
cujo  -ésimo elemento é
-ésimo elemento é  ,
,  .
.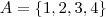 e
e  .
. 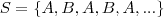 . Se imaginarmos que
. Se imaginarmos que  e
e  são, na verdade, números reais quaisquer então
são, na verdade, números reais quaisquer então ![S_n = \frac{1}{2}[A+B+(B-A)(-1)^n] S_n = \frac{1}{2}[A+B+(B-A)(-1)^n]](/latexrender/pictures/411faba419cd454a1334c7a96d9066e8.png)
![S_n \in \frac{1}{2}[A+B+(B-A)(-1)^n] S_n \in \frac{1}{2}[A+B+(B-A)(-1)^n]](/latexrender/pictures/086ac27a6012c80ad6552557aee664eb.png) . Isto é, o
. Isto é, o  -ésimo termo pertencerá a prevista subsequência. É interessante notar aqui que o "4" de A é diferente do "4" de B. Em geral, é como se as subsequências tivessem elementos todos diferentes.
-ésimo termo pertencerá a prevista subsequência. É interessante notar aqui que o "4" de A é diferente do "4" de B. Em geral, é como se as subsequências tivessem elementos todos diferentes.  -ésimo termo da sequência vai pertencer. Ainda, como ambas subsequências tem 4 elementos, cada vez que
-ésimo termo da sequência vai pertencer. Ainda, como ambas subsequências tem 4 elementos, cada vez que  for múltiplo de 4 o
for múltiplo de 4 o  será 4 se
será 4 se 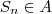 e 1 se
e 1 se  . Daí, se
. Daí, se  é o resto da divisão de
é o resto da divisão de  por 4, então
por 4, então  será o
será o 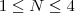 termo de
termo de  ou
ou  .
. tem resto
tem resto  e
e 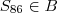 , então
, então 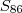 é o 2° termo de
é o 2° termo de  que é 3.
que é 3.
Russman escreveu:Trata-se de uma sequência periódica. Não é tão simples pq dentro do período há termos repetidos. Eu pensei em resolver da seguinte forma.
Seja a sequênciacujo
-ésimo elemento é
,
.
Tome duas subsequênciase
.
Assim, podemos escrever. Se imaginarmos que
e
são, na verdade, números reais quaisquer então
Escrevendo formalmente, temos. Isto é, o
-ésimo termo pertencerá a prevista subsequência. É interessante notar aqui que o "4" de A é diferente do "4" de B. Em geral, é como se as subsequências tivessem elementos todos diferentes.
Portanto, agora podemos prever em qual sub-sequência que o-ésimo termo da sequência vai pertencer. Ainda, como ambas subsequências tem 4 elementos, cada vez que
for múltiplo de 4 o
será 4 se
e 1 se
. Daí, se
é o resto da divisão de
por 4, então
será o
termo de
ou
.
Comotem resto
e
, então
é o 2° termo de
que é 3.
(:

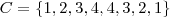 , então
, então  . Daí, como
. Daí, como  tem 8 termos, se o resto da divisão
tem 8 termos, se o resto da divisão 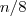 é
é 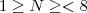 então o
então o  será o
será o  -ésimo termo de
-ésimo termo de  .
. por 4 ao invés de 8, que parece mais fácil! hahaha brincadeira.
por 4 ao invés de 8, que parece mais fácil! hahaha brincadeira.


Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.