 por wesley franciz » Seg Abr 21, 2014 20:15
por wesley franciz » Seg Abr 21, 2014 20:15

- Questão
Galera eu só achei um linha que é: 123
4 ---- 432
1 ---- 123
4 ---- 432
1------------Posições nos números:
Primeiro -- Segundo -- Terceiro -- Quarto Percebi que os números de ordem ímpar terminam em Par que é o
4 e os de ordem Par terminam em ìmpar que é o
1Estão marquei a letra D) 1, pq o 86 termo é Par.
Ainda não saiu o gabarito oficial, vcs veem outra R.L nessa questão? afinal o resultado é a letra
B) 3Obrigado.
-
wesley franciz
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qua Jan 02, 2013 13:13
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Russman » Seg Abr 21, 2014 22:07
por Russman » Seg Abr 21, 2014 22:07
Trata-se de uma sequência periódica. Não é tão simples resolver pois o período é 8 e teríamos de resolver uma equação polinomial de 8° grau. Dá pra fazer. Mas eu pensei, alternativamente, vista simetria do período(parece redundante essa expressão) em resolver da seguinte forma.
Seja a sequência
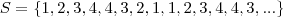
cujo

-ésimo elemento é

,

.
Tome duas subsequências
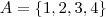
e

.
Assim, podemos escrever
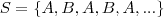
. Se imaginarmos que

e

são, na verdade, números reais quaisquer então
![S_n = \frac{1}{2}[A+B+(B-A)(-1)^n] S_n = \frac{1}{2}[A+B+(B-A)(-1)^n]](/latexrender/pictures/411faba419cd454a1334c7a96d9066e8.png)
Escrevendo formalmente, temos
![S_n \in \frac{1}{2}[A+B+(B-A)(-1)^n] S_n \in \frac{1}{2}[A+B+(B-A)(-1)^n]](/latexrender/pictures/086ac27a6012c80ad6552557aee664eb.png)
. Isto é, o

-ésimo termo pertencerá a prevista subsequência. É interessante notar aqui que o "4" de A é diferente do "4" de B. Em geral, é como se as subsequências tivessem elementos todos diferentes.
Portanto, agora podemos prever em qual sub-sequência que o

-ésimo termo da sequência vai pertencer. Ainda, como ambas subsequências tem 4 elementos, cada vez que

for múltiplo de 4 o

será 4 se
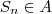
e 1 se

. Daí, se

é o resto da divisão de

por 4, então

será o
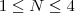
termo de

ou

.
Como

tem resto

e
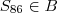
, então
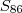
é o 2° termo de

que é
3.
(:
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por wesley franciz » Seg Abr 21, 2014 22:21
por wesley franciz » Seg Abr 21, 2014 22:21
Russman escreveu:Trata-se de uma sequência periódica. Não é tão simples pq dentro do período há termos repetidos. Eu pensei em resolver da seguinte forma.
Seja a sequência
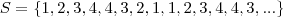
cujo

-ésimo elemento é

,

.
Tome duas subsequências
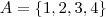
e

.
Assim, podemos escrever
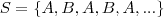
. Se imaginarmos que

e

são, na verdade, números reais quaisquer então
![S_n = \frac{1}{2}[A+B+(B-A)(-1)^n] S_n = \frac{1}{2}[A+B+(B-A)(-1)^n]](/latexrender/pictures/411faba419cd454a1334c7a96d9066e8.png)
Escrevendo formalmente, temos
![S_n \in \frac{1}{2}[A+B+(B-A)(-1)^n] S_n \in \frac{1}{2}[A+B+(B-A)(-1)^n]](/latexrender/pictures/086ac27a6012c80ad6552557aee664eb.png)
. Isto é, o

-ésimo termo pertencerá a prevista subsequência. É interessante notar aqui que o "4" de A é diferente do "4" de B. Em geral, é como se as subsequências tivessem elementos todos diferentes.
Portanto, agora podemos prever em qual sub-sequência que o

-ésimo termo da sequência vai pertencer. Ainda, como ambas subsequências tem 4 elementos, cada vez que

for múltiplo de 4 o

será 4 se
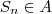
e 1 se

. Daí, se

é o resto da divisão de

por 4, então

será o
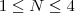
termo de

ou

.
Como

tem resto

e
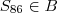
, então
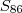
é o 2° termo de

que é
3.
(:
Muito obrigado, vou separar um tempo pra fazer desse jeito umas dez vezes, até pegar a senha,kkkk
Vi na internet uma pessoa colocou assim:
86 | 8_____
8. . 10
. 6
86º = 1, 2, 3, 4, 4, (3) <= 3 <= a resposta
Mas não explicou o processo. É o msm Raciocínio seu?
-
wesley franciz
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qua Jan 02, 2013 13:13
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Russman » Seg Abr 21, 2014 22:42
por Russman » Seg Abr 21, 2014 22:42
É, o mesmo raciocínio. Mas nesse caso a pessoa usou o período todo, que é 8. Se fizermos
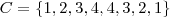
, então

. Daí, como

tem 8 termos, se o resto da divisão
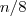
é
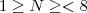
então o

será o

-ésimo termo de

.
Parece mais simples fazer assim do que dividir a sequência em 2. A vantagem em dividir a sequência em 2 é que temos de dividir

por 4 ao invés de 8, que parece mais fácil! hahaha brincadeira.
Mas, de fato, resolver por Equações de Diferenças Finitas seria BEM mais elegante do que esse monte de suposições.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por wesley franciz » Seg Abr 21, 2014 23:13
por wesley franciz » Seg Abr 21, 2014 23:13
Vou treina mais na sua resolução msm, pq tem mais base,kkk. No dia da prova vai ficar por último, a banca IBFC sempre compra um questões assim e sempre é fácil o raciocínio, mas nas últimas prova ela está pegando mais pesado,kkkkk.
Muito Obrigado.
-
wesley franciz
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qua Jan 02, 2013 13:13
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Russman » Seg Abr 21, 2014 23:20
por Russman » Seg Abr 21, 2014 23:20
Não por isso. Boa sorte. (:
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Lógica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Teoria Números] Algoritmo Não Interceptação Números Primos
por WillamesSilva » Qua Out 26, 2016 12:21
- 8 Respostas
- 17193 Exibições
- Última mensagem por WillamesSilva

Ter Nov 22, 2016 15:33
Aritmética
-
- Números complexos módulo de dois números complexos important
por elisamaria » Qui Jun 11, 2015 16:56
- 1 Respostas
- 17114 Exibições
- Última mensagem por nakagumahissao

Qui Jun 11, 2015 19:20
Números Complexos
-
- Números Reais - Simplificar números reais
por ZANGARO » Ter Nov 15, 2011 18:46
- 0 Respostas
- 1947 Exibições
- Última mensagem por ZANGARO

Ter Nov 15, 2011 18:46
Álgebra Elementar
-
- Numeros complexos!
por Estela » Seg Mar 17, 2008 00:57
- 7 Respostas
- 13351 Exibições
- Última mensagem por andegledson

Seg Nov 02, 2009 21:41
Números Complexos
-
- Números Complexos
por michelle » Dom Ago 31, 2008 15:35
- 3 Respostas
- 10330 Exibições
- Última mensagem por admin

Dom Ago 31, 2008 21:00
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



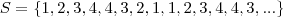 cujo
cujo  -ésimo elemento é
-ésimo elemento é  ,
,  .
.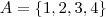 e
e  .
. 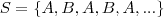 . Se imaginarmos que
. Se imaginarmos que  e
e  são, na verdade, números reais quaisquer então
são, na verdade, números reais quaisquer então ![S_n = \frac{1}{2}[A+B+(B-A)(-1)^n] S_n = \frac{1}{2}[A+B+(B-A)(-1)^n]](/latexrender/pictures/411faba419cd454a1334c7a96d9066e8.png)
![S_n \in \frac{1}{2}[A+B+(B-A)(-1)^n] S_n \in \frac{1}{2}[A+B+(B-A)(-1)^n]](/latexrender/pictures/086ac27a6012c80ad6552557aee664eb.png) . Isto é, o
. Isto é, o  -ésimo termo pertencerá a prevista subsequência. É interessante notar aqui que o "4" de A é diferente do "4" de B. Em geral, é como se as subsequências tivessem elementos todos diferentes.
-ésimo termo pertencerá a prevista subsequência. É interessante notar aqui que o "4" de A é diferente do "4" de B. Em geral, é como se as subsequências tivessem elementos todos diferentes.  -ésimo termo da sequência vai pertencer. Ainda, como ambas subsequências tem 4 elementos, cada vez que
-ésimo termo da sequência vai pertencer. Ainda, como ambas subsequências tem 4 elementos, cada vez que  for múltiplo de 4 o
for múltiplo de 4 o  será 4 se
será 4 se 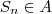 e 1 se
e 1 se  . Daí, se
. Daí, se  é o resto da divisão de
é o resto da divisão de  por 4, então
por 4, então  será o
será o 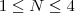 termo de
termo de  ou
ou  .
. tem resto
tem resto  e
e 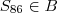 , então
, então 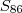 é o 2° termo de
é o 2° termo de  que é 3.
que é 3.
cujo
-ésimo elemento é
,
.
e
.
. Se imaginarmos que
e
são, na verdade, números reais quaisquer então
. Isto é, o
-ésimo termo pertencerá a prevista subsequência. É interessante notar aqui que o "4" de A é diferente do "4" de B. Em geral, é como se as subsequências tivessem elementos todos diferentes.
-ésimo termo da sequência vai pertencer. Ainda, como ambas subsequências tem 4 elementos, cada vez que
for múltiplo de 4 o
será 4 se
e 1 se
. Daí, se
é o resto da divisão de
por 4, então
será o
termo de
ou
.
tem resto
e
, então
é o 2° termo de
que é 3.

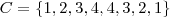 , então
, então  . Daí, como
. Daí, como  tem 8 termos, se o resto da divisão
tem 8 termos, se o resto da divisão 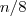 é
é 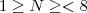 então o
então o  será o
será o  -ésimo termo de
-ésimo termo de  .
. por 4 ao invés de 8, que parece mais fácil! hahaha brincadeira.
por 4 ao invés de 8, que parece mais fácil! hahaha brincadeira.


 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: } você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais? } você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?