Preciso saber como cacular a e b dando o limite
limite x tende a 1
a raiz x + 1 - b divide x -1 = raiz de 2 , preciso achar a e b. eu não conseguir escrever nas formulas.




![\lim_{x\to1} a \frac{\sqrt[]{x+1}}{x-1}- b =\sqrt[]{2} \lim_{x\to1} a \frac{\sqrt[]{x+1}}{x-1}- b =\sqrt[]{2}](/latexrender/pictures/f18e050593a00bffbe3491ed89899ed6.png)

santhiago escreveu:Utilize o site http://www.codecogs.com/latex/eqneditor.php , veja a tabela , com o passar do tempo aprenderá os códigos . Muito difícil entender a expressão .

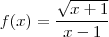 , temos
, temos  não está definida em x = 1, mas ela está definida em
não está definida em x = 1, mas ela está definida em 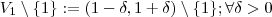 suficientemente pequeno e esta função não é limitada neste conjunto .
suficientemente pequeno e esta função não é limitada neste conjunto .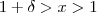
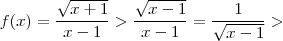 . Por outro lado ,
. Por outro lado , 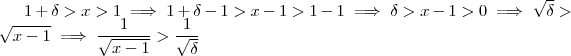 .Desta forma ,
.Desta forma ,  sempre que
sempre que 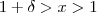
 arbitrário suficientemente pequeno , a função avaliada em
arbitrário suficientemente pequeno , a função avaliada em  será sempre maior que o número
será sempre maior que o número  suficientemente grande desde que
suficientemente grande desde que  ..
..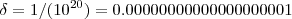 .
.  sempre que
sempre que 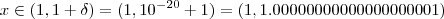
 suficientemente grande e
suficientemente grande e  .
.  , imponha que
, imponha que 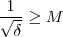 . Para isto , basta que
. Para isto , basta que  , e assim
, e assim 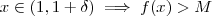 .
. ,teremos sempre
,teremos sempre 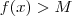 , para isto basta que
, para isto basta que  .
.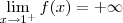 .
.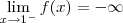 .
. . Se
. Se  ,
,  não é limitada em
não é limitada em  .
.  .
.  ,
, 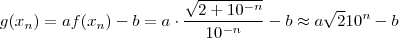 .
. na vizinhança de
na vizinhança de  .
.
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)

 então
então  .
. 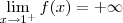 . Lembra ?
. Lembra ?  .
. 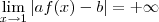 .
.  (certo ??) tal que
(certo ??) tal que  . Pondo
. Pondo 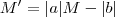 temos
temos 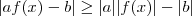 (desigualdade triangular) .
(desigualdade triangular) .  para
para  então também vale
então também vale 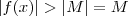 .Assim , obtemos
.Assim , obtemos 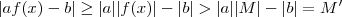 .
.  .
.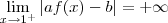 logo
logo 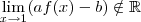 .
.
 e
e  é sacanagem! hahaha
é sacanagem! hahaha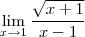 depende se tendemos
depende se tendemos  a
a  pela direita o esquerda. Começando mal por aí. Calculando os limites laterias obtemos
pela direita o esquerda. Começando mal por aí. Calculando os limites laterias obtemos  que não é uma indeterminação. A única forma de ser, seria tendo algo( no caso o real
que não é uma indeterminação. A única forma de ser, seria tendo algo( no caso o real  ) multiplicando o numerador para resultar em
) multiplicando o numerador para resultar em  .
.

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
