 por uefs » Qui Abr 17, 2014 00:23
por uefs » Qui Abr 17, 2014 00:23
Preciso saber como cacular a e b dando o limite
limite x tende a 1
a raiz x + 1 - b divide x -1 = raiz de 2 , preciso achar a e b. eu não conseguir escrever nas formulas.
-
uefs
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Abr 17, 2014 00:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por e8group » Qui Abr 17, 2014 23:38
por e8group » Qui Abr 17, 2014 23:38
Utilize o site
http://www.codecogs.com/latex/eqneditor.php , veja a tabela , com o passar do tempo aprenderá os códigos . Muito difícil entender a expressão .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por uefs » Sáb Abr 19, 2014 01:28
por uefs » Sáb Abr 19, 2014 01:28
![\lim_{x\to1} a \frac{\sqrt[]{x+1}}{x-1}- b =\sqrt[]{2} \lim_{x\to1} a \frac{\sqrt[]{x+1}}{x-1}- b =\sqrt[]{2}](/latexrender/pictures/f18e050593a00bffbe3491ed89899ed6.png)
por favor preciso resolver esse limete, preciso dos valores de a e b, como achar
-
uefs
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Abr 17, 2014 00:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por uefs » Sáb Abr 19, 2014 01:35
por uefs » Sáb Abr 19, 2014 01:35
conseguir , por favor tente reponder para mim ajudar
-
uefs
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Abr 17, 2014 00:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por e8group » Sáb Abr 19, 2014 13:21
por e8group » Sáb Abr 19, 2014 13:21
Vou tentar ajudar .
Considere
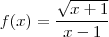
, temos

não está definida em x = 1, mas ela está definida em
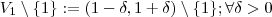
suficientemente pequeno e esta função não é limitada neste conjunto .
Ora tome
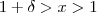
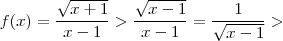
. Por outro lado ,
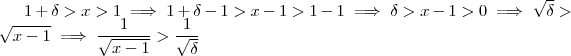
.Desta forma ,

sempre que
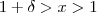
Olha que interessante que acabamos de mostrar , dado

arbitrário suficientemente pequeno , a função avaliada em

será sempre maior que o número

suficientemente grande desde que

..
Exemplo :
Se tomarmos
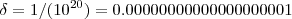
.

sempre que
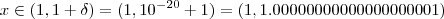
Também podemos , obter uma relação entre

suficientemente grande e

.
Ora, dado

, imponha que
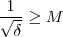
. Para isto , basta que

, e assim
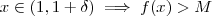
.
Não importa o quão grande seja

,teremos sempre
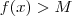
, para isto basta que

.
Toda o raciocínio acima nos diz que
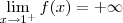
.
E também sabemos que
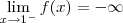
.
Agora defina

. Se

,

não é limitada em

.
Exemplo :
Defina

.
Agora avaliamos a função em

,
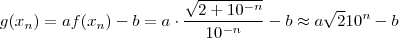
.
Dependendo do sinal de a , a aproximação será com excesso , ou falta .
Isto não prova nada , mas nos dá uma ideia intuitiva do comportamento de

na vizinhança de

.
Acho que já dá p/ perceber que é a e b .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por uefs » Sáb Abr 19, 2014 15:40
por uefs » Sáb Abr 19, 2014 15:40
Não entendir, pois na questão ele pede os valores de a e b, a resposta é a=4 e b= 4
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
-
uefs
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Abr 17, 2014 00:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por e8group » Sáb Abr 19, 2014 17:03
por e8group » Sáb Abr 19, 2014 17:03
Negativo . Resposta errada .
Se quiser conferir computacionalmente
http://www.wolframalpha.com/input/?i=li ... s+x+to+1++ .
Agora matematicamente , vou mostra que se

então

.
Já mostramos que
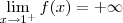
. Lembra ?

.
Pois bem , agora vamos mostra que
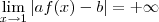
.
Podemos escolher

(certo ??) tal que

. Pondo
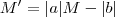
temos
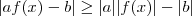
(desigualdade triangular) .
Além disso , se

para

então também vale
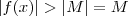
.Assim , obtemos
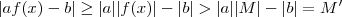
.
O que prova que

.
Ora se
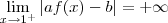
logo
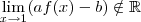
.
Portanto devemos ter a = 0 .
P.S. Não estou 100% certo que eu disse acima faz sentido ...
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Russman » Sáb Abr 19, 2014 19:48
por Russman » Sáb Abr 19, 2014 19:48
Resolver para

e

é sacanagem! hahaha
Mas, de fato, é uma solução trivial e, concordando com o santhiago, a única.
A questão é estranha. O resultado de
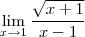
depende se tendemos

a

pela direita o esquerda. Começando mal por aí. Calculando os limites laterias obtemos

que não é uma indeterminação. A única forma de ser, seria tendo algo( no caso o real

) multiplicando o numerador para resultar em

.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por e8group » Sáb Abr 19, 2014 21:24
por e8group » Sáb Abr 19, 2014 21:24
Mais uma pessoa em concordância ... Isto é bom .
uefs faz o favor de conferir se digitou corretamente a expressão . Como vc não está familiarizado com o LaTeX bem provável erros .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Como calcular derivadas com a constante "e"
por fer_carnie » Seg Jun 20, 2011 20:40
- 1 Respostas
- 2081 Exibições
- Última mensagem por Fabio Cabral

Seg Jun 20, 2011 22:22
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Calcular esse limite
 por ViniciusAlmeida » Sáb Abr 18, 2015 08:45
por ViniciusAlmeida » Sáb Abr 18, 2015 08:45
- 1 Respostas
- 1907 Exibições
- Última mensagem por adauto martins

Qui Mai 07, 2015 13:02
Cálculo: Limites, Derivadas e Integrais
-
- CALCULAR LIMITE
por Michelee » Dom Mai 01, 2011 12:04
- 3 Respostas
- 3105 Exibições
- Última mensagem por LuizAquino

Dom Mai 01, 2011 19:01
Cálculo: Limites, Derivadas e Integrais
-
- Calcular limite
por LAZAROTTI » Ter Mai 01, 2012 13:56
- 1 Respostas
- 1352 Exibições
- Última mensagem por LuizAquino

Ter Mai 01, 2012 14:55
Cálculo: Limites, Derivadas e Integrais
-
- Calcular o limite de
por nowfeer » Seg Jun 18, 2012 01:22
- 2 Respostas
- 1840 Exibições
- Última mensagem por nowfeer

Ter Jun 19, 2012 21:36
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




![\lim_{x\to1} a \frac{\sqrt[]{x+1}}{x-1}- b =\sqrt[]{2} \lim_{x\to1} a \frac{\sqrt[]{x+1}}{x-1}- b =\sqrt[]{2}](/latexrender/pictures/f18e050593a00bffbe3491ed89899ed6.png)


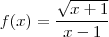 , temos
, temos  não está definida em x = 1, mas ela está definida em
não está definida em x = 1, mas ela está definida em 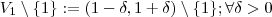 suficientemente pequeno e esta função não é limitada neste conjunto .
suficientemente pequeno e esta função não é limitada neste conjunto .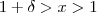
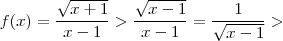 . Por outro lado ,
. Por outro lado , 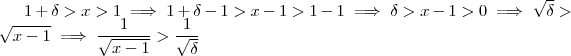 .Desta forma ,
.Desta forma ,  sempre que
sempre que 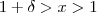
 arbitrário suficientemente pequeno , a função avaliada em
arbitrário suficientemente pequeno , a função avaliada em  será sempre maior que o número
será sempre maior que o número  suficientemente grande desde que
suficientemente grande desde que  ..
..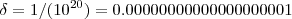 .
.  sempre que
sempre que 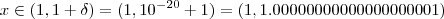
 suficientemente grande e
suficientemente grande e  .
.  , imponha que
, imponha que 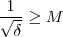 . Para isto , basta que
. Para isto , basta que  , e assim
, e assim 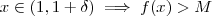 .
. ,teremos sempre
,teremos sempre 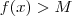 , para isto basta que
, para isto basta que  .
.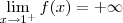 .
.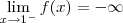 .
. . Se
. Se  ,
,  não é limitada em
não é limitada em  .
.  .
.  ,
, 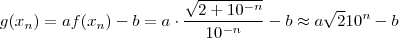 .
. na vizinhança de
na vizinhança de  .
.
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)

 então
então  .
. 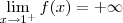 . Lembra ?
. Lembra ?  .
. 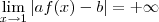 .
.  (certo ??) tal que
(certo ??) tal que  . Pondo
. Pondo 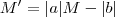 temos
temos 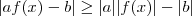 (desigualdade triangular) .
(desigualdade triangular) .  para
para  então também vale
então também vale 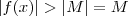 .Assim , obtemos
.Assim , obtemos 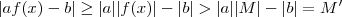 .
.  .
.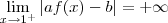 logo
logo 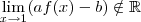 .
.
 e
e  é sacanagem! hahaha
é sacanagem! hahaha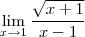 depende se tendemos
depende se tendemos  a
a  pela direita o esquerda. Começando mal por aí. Calculando os limites laterias obtemos
pela direita o esquerda. Começando mal por aí. Calculando os limites laterias obtemos  que não é uma indeterminação. A única forma de ser, seria tendo algo( no caso o real
que não é uma indeterminação. A única forma de ser, seria tendo algo( no caso o real  ) multiplicando o numerador para resultar em
) multiplicando o numerador para resultar em  .
.



 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.