Boa Noite.
Sabendo que 2 sen x + 5 cos x = 0 e que pi/2<x<pi, obtenha o valor de sen x e cos x.
Estou com dúvidas na resolução da equação acima. Resolvi cheguei a um número muito estranho para cosx e sen x mas no enunciado o intervalo corresponde a cosx negativo e senx positivo. Encontrei exatamente o contrário. Podem me ajudar, por favor?
Obrigada.


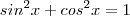 .
.  . A função cosseno é sempre negativa neste intervalo ,logo
. A função cosseno é sempre negativa neste intervalo ,logo  .
. 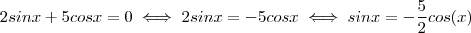 . Podemos dividir ambos membros
. Podemos dividir ambos membros 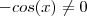 ,
, 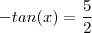 . Como ambos membros é positivo , elevando ao quadrado
. Como ambos membros é positivo , elevando ao quadrado  . Porém sabemos q
. Porém sabemos q  .
.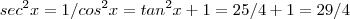 . Logo
. Logo 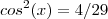 ou seja
ou seja  . Como
. Como  , obtemos
, obtemos 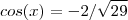 .
.
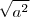 não é
não é  e sim
e sim  . Logo , se
. Logo , se  ,
,  . Caso , a > 0 ou a = 0 ,
. Caso , a > 0 ou a = 0 , ![|a| = a . Neste caso sim [tex] \sqrt{a^2} = a |a| = a . Neste caso sim [tex] \sqrt{a^2} = a](/latexrender/pictures/1a6f2a5ea11181b15f04b0ad004e0aaa.png) .
.