 por Andre Arruda » Ter Mar 25, 2014 16:55
por Andre Arruda » Ter Mar 25, 2014 16:55
Olá! Estava olhando provas anteriores de minha universidade e vi uma questão sobre matrizes que pedia para falar se algumas afirmativas feitas eram verdadeiras ou falsas com justificativa. Nessa afirmação:
"Se

é uma matriz

x

tal que
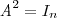
, então
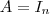
ou
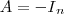
"
Bom, como uma matriz multiplicada pela sua inversa sempre dá a matriz identidade, imaginei que a afirmação seja falsa, uma vez que para que
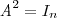
,

.
Não sei, entretanto, como colocar isso na resposta caso apareça em uma prova (ou qualquer questão similar) e se teria que exemplificar com um caso numérico para prova. É meu primeiro semestre na universidade, então não tenho muita noção de como funciona isso. Se alguém puder ajudar com essa ideia, agradeço muito!
-
Andre Arruda
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Mar 25, 2014 16:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: cursando
 por e8group » Qui Mar 27, 2014 12:32
por e8group » Qui Mar 27, 2014 12:32
Bom dia . A implicação não necessariamente é verdadeira . Se fosse , ela valeria para todo

natural .Negar a afirmação entre aspas é o suficiente mostrar um contra exemplo . Vamos escolher n = 2 para simplificar e mostra que existe outra matriz

inversível diferente de

tal que

.Comece escrevendo
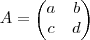
(vamos determinar a,b,c,d ) . Segue-se

.
Desde que

, então

e

.
Dá segunda relação ,temos
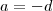
e

quaisquer .
Mas ,
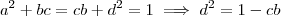
. Como
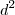
é sempre positivo , o lado direito também o é , escolhendo-se então
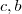
reais tais que
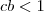
a solução geral do sistema será

com
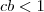
.
Agora podemos encontrar quantas matrizes quisermos , basta tomar valores para
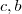
de modo que
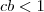
. Exemplo , escolha

e
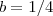
.Temos
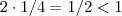
e
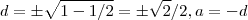
Disso temos uma matriz

tal que

.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Andre Arruda » Qui Mar 27, 2014 17:28
por Andre Arruda » Qui Mar 27, 2014 17:28
Certo, muito obrigado, Santhiago! Me ajudou bastante, acho que peguei a ideia de como justificar, vou treinar mais isso. Mais uma vez, muito obrigado.
-
Andre Arruda
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Mar 25, 2014 16:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: cursando
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Matrizes] Comentar uma afirmação
por fff » Sex Out 10, 2014 07:56
- 0 Respostas
- 2432 Exibições
- Última mensagem por fff

Sex Out 10, 2014 07:56
Matrizes e Determinantes
-
- verificação espaço vetor.
por amr » Qua Abr 06, 2011 12:15
- 0 Respostas
- 1431 Exibições
- Última mensagem por amr

Qua Abr 06, 2011 12:15
Introdução à Álgebra Linear
-
- [Verificação de Espaço Vetorial]
por Engenet » Qua Jan 11, 2017 13:36
- 1 Respostas
- 1985 Exibições
- Última mensagem por Engenet

Qui Jan 12, 2017 21:02
Álgebra Linear
-
- Justificar a afirmação
 por silvanuno11 » Sex Mai 25, 2012 12:45
por silvanuno11 » Sex Mai 25, 2012 12:45
- 2 Respostas
- 4118 Exibições
- Última mensagem por silvanuno11

Seg Mai 28, 2012 06:36
Binômio de Newton
-
- Justificar a afirmação
 por silvanuno11 » Dom Mai 27, 2012 16:30
por silvanuno11 » Dom Mai 27, 2012 16:30
- 1 Respostas
- 1625 Exibições
- Última mensagem por PeterHiggs

Qui Mai 31, 2012 11:22
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 é uma matriz
é uma matriz  x
x  tal que
tal que 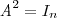 , então
, então 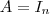 ou
ou 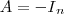 "
"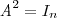 ,
,  .
.

 natural .Negar a afirmação entre aspas é o suficiente mostrar um contra exemplo . Vamos escolher n = 2 para simplificar e mostra que existe outra matriz
natural .Negar a afirmação entre aspas é o suficiente mostrar um contra exemplo . Vamos escolher n = 2 para simplificar e mostra que existe outra matriz  inversível diferente de
inversível diferente de  tal que
tal que  .Comece escrevendo
.Comece escrevendo 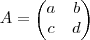 (vamos determinar a,b,c,d ) . Segue-se
(vamos determinar a,b,c,d ) . Segue-se  .
.  e
e  .
.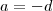 e
e  quaisquer .
quaisquer . 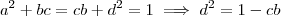 . Como
. Como 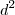 é sempre positivo , o lado direito também o é , escolhendo-se então
é sempre positivo , o lado direito também o é , escolhendo-se então 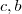 reais tais que
reais tais que 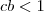 a solução geral do sistema será
a solução geral do sistema será  com
com 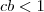 .
. e
e 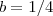 .Temos
.Temos 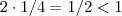 e
e 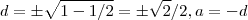
 tal que
tal que 
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
