 por zanotto » Sex Mar 21, 2014 23:18
por zanotto » Sex Mar 21, 2014 23:18
h(x) = ln(1 + sen²(x))
Determine fun�ção f e g tais que h = g(f(x)).
Não consigo fazer.
-
zanotto
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Mar 21, 2014 23:10
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Russman » Sáb Mar 22, 2014 00:54
por Russman » Sáb Mar 22, 2014 00:54
Uma possível resposta é
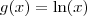
e
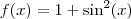
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por zanotto » Sáb Mar 22, 2014 01:13
por zanotto » Sáb Mar 22, 2014 01:13
Tem como demostrar os cálculos?
-
zanotto
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Mar 21, 2014 23:10
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Russman » Sáb Mar 22, 2014 01:22
por Russman » Sáb Mar 22, 2014 01:22
Não tem cálculo. É só olhar pra
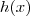
e ver qual função que está "dentro" de outra.
Por exemplo, se
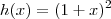
. Então, teríamos
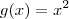
e
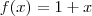
, pois

nada mais é do que substituir o "

" da

por

.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- questão função
por sheila » Qui Set 06, 2007 22:37
- 4 Respostas
- 7820 Exibições
- Última mensagem por admin

Ter Set 11, 2007 16:39
Funções
-
- Questão de Funçao
por kael » Qui Mar 05, 2009 16:30
- 4 Respostas
- 2978 Exibições
- Última mensagem por Molina

Sex Mar 06, 2009 12:47
Funções
-
- Questao de Funçao
por leilahomsi » Qua Jan 09, 2013 19:19
- 1 Respostas
- 1310 Exibições
- Última mensagem por e8group

Qua Jan 09, 2013 22:38
Funções
-
- QUESTÃO DE FUNÇÃO DA UFJF
por Maira » Sáb Dez 19, 2009 16:47
- 3 Respostas
- 3031 Exibições
- Última mensagem por Maira

Sáb Dez 19, 2009 19:27
Funções
-
- Questão de Função (UFRJ)
por Carolziiinhaaah » Qui Ago 12, 2010 11:34
- 1 Respostas
- 2729 Exibições
- Última mensagem por Douglasm

Qui Ago 12, 2010 13:14
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





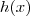 e ver qual função que está "dentro" de outra.
e ver qual função que está "dentro" de outra.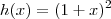 . Então, teríamos
. Então, teríamos 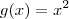 e
e 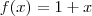 , pois
, pois  nada mais é do que substituir o "
nada mais é do que substituir o " " da
" da  por
por  .
.