 por Bielto » Dom Mar 16, 2014 17:40
por Bielto » Dom Mar 16, 2014 17:40
boa tarde,
Eu resolvi um exercício porem o meu resultado não bate com o gabarito.
Esta pedindo para encontrar a forma mais simples dessa expressão
![\[\frac{49^-^6.343^-^3}{(7^2)^-^3.\frac{1}{7}^-^7}\] \[\frac{49^-^6.343^-^3}{(7^2)^-^3.\frac{1}{7}^-^7}\]](/latexrender/pictures/d57f4846c4579330e11f282084129c98.png)
Resposta do Gabarito:
![\[7^-^8\] \[7^-^8\]](/latexrender/pictures/75fa207eee8580e5aaae3ebf07cba495.png)
Minha resposta:
![\[7^-^2^2\] \[7^-^2^2\]](/latexrender/pictures/94913510da28c8f30216a44499b36d50.png)
E minha resolução:
![\[\frac{(7^2)^-^6.(7^3)^-^3}{(7^2)^-^3.7^7} = \frac{7^-^1^2.7^-^9}{7^-^6.7^7} = \frac{7^-^2^1}{7^1} = 7^-^2^1^-^(^+^1^)=7^2^2\] \[\frac{(7^2)^-^6.(7^3)^-^3}{(7^2)^-^3.7^7} = \frac{7^-^1^2.7^-^9}{7^-^6.7^7} = \frac{7^-^2^1}{7^1} = 7^-^2^1^-^(^+^1^)=7^2^2\]](/latexrender/pictures/127c618ce2352602a64cd10a06f53e56.png)
-
Bielto
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Qui Jul 12, 2012 15:07
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Médio
- Andamento: formado
 por Cleyson007 » Dom Mar 16, 2014 18:09
por Cleyson007 » Dom Mar 16, 2014 18:09
Bielto, não há erro em sua resolução!
Para você encontrar a resposta do gabarito deverá ter no denominador
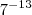
. Daí, suponho que não seja um sétimo elevado a -7, mas
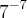
Abraço,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Bielto » Dom Mar 16, 2014 18:38
por Bielto » Dom Mar 16, 2014 18:38
Cleyson007 escreveu:Bielto, não há erro em sua resolução!
Para você encontrar a resposta do gabarito deverá ter no denominador
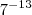
. Daí, suponho que não seja um sétimo elevado a -7, mas
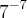
Abraço,
Cleyson007
Boa tarde Cleyson, então o exercício é realmente
![\[\frac{1}{7}^-^7\] \[\frac{1}{7}^-^7\]](/latexrender/pictures/f7c8bf703481ccf8bc3097f121d6f660.png)
e não
![\[7^-^7\] \[7^-^7\]](/latexrender/pictures/6ff979f4933e6554c2809f4c41bdcc63.png)
-
Bielto
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Qui Jul 12, 2012 15:07
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Médio
- Andamento: formado
 por Cleyson007 » Dom Mar 16, 2014 18:43
por Cleyson007 » Dom Mar 16, 2014 18:43
Não vejo erro na resposta
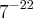
Acredito que há um erro em seu gabarito.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Bielto » Dom Mar 16, 2014 18:46
por Bielto » Dom Mar 16, 2014 18:46
Cleyson007 escreveu:Não vejo erro na resposta
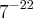
Acredito que há um erro em seu gabarito.
Por favor, veja isso
http://pir2.forumeiros.com/t65438-expressaoMe desculpe se estou sendo inconveniente mas por favor, olha a resposta do velho.
-
Bielto
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Qui Jul 12, 2012 15:07
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Médio
- Andamento: formado
 por Cleyson007 » Dom Mar 16, 2014 19:20
por Cleyson007 » Dom Mar 16, 2014 19:20
Bielto, pelo que entendi é o seguinte:
Para se ter o resultado de 7^-8 devemos ter (1/7)^7 no denominador.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Bielto » Dom Mar 16, 2014 19:28
por Bielto » Dom Mar 16, 2014 19:28
Cara, olha o que me disseram
"
Isso depende.
(1/7)^{-7} = 7^7
[1^{-7}]/7 = 1/7
Veja bem isso."
Vou colocar em imagens para facilitar a compreensão
![\[\left ( \frac{1}{7} \right )^-^7 = \frac{7}{7}\] \[\left ( \frac{1}{7} \right )^-^7 = \frac{7}{7}\]](/latexrender/pictures/c2a948702f5cecf47df70a89e938b915.png)
e que
![\[\frac{1^(^-^7^)}{7}= \frac{1}{7}\] \[\frac{1^(^-^7^)}{7}= \frac{1}{7}\]](/latexrender/pictures/096c7c7a5b27ae0941cf8c5dd31f3d05.png)
Está correto isso? Eu aprendi que
![\[\left ( \frac{1}{7} \right )^-^7 = \left (\frac{7}{1}\right )^7\] \[\left ( \frac{1}{7} \right )^-^7 = \left (\frac{7}{1}\right )^7\]](/latexrender/pictures/93c63c1cc09ebb5ac7bfff7047344f78.png)
e que
![\[\frac{1^(^-^7^)}{7}= -\frac{1}{7}\] \[\frac{1^(^-^7^)}{7}= -\frac{1}{7}\]](/latexrender/pictures/4e18aaed643018f978a2586e3547cda6.png)
-
Bielto
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Qui Jul 12, 2012 15:07
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Médio
- Andamento: formado
 por Bielto » Dom Mar 16, 2014 19:35
por Bielto » Dom Mar 16, 2014 19:35
Cleyson007 escreveu:Bielto, pelo que entendi é o seguinte:
Para se ter o resultado de 7^-8 devemos ter (1/7)^7 no denominador.
Desculpe, mas não tem como fazer isso pois no exercício está (1/7)^-7 no denominador.
-
Bielto
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Qui Jul 12, 2012 15:07
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Médio
- Andamento: formado
Voltar para Aritmética
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Uma expressao simples
por Jem - » Sáb Jan 09, 2010 18:37
- 2 Respostas
- 1462 Exibições
- Última mensagem por Jem -

Sáb Jan 09, 2010 18:57
Álgebra Elementar
-
- Expressão aparentemente simples, porém...
por Alexander » Qua Dez 01, 2010 15:50
- 5 Respostas
- 4497 Exibições
- Última mensagem por Alexander

Qui Dez 02, 2010 22:09
Sistemas de Equações
-
- Expressão
por geriane » Qui Abr 22, 2010 12:49
- 4 Respostas
- 3882 Exibições
- Última mensagem por geriane

Sáb Abr 24, 2010 10:50
Trigonometria
-
- Expressão em PG
por Carolziiinhaaah » Qua Jun 16, 2010 21:10
- 1 Respostas
- 2005 Exibições
- Última mensagem por MarceloFantini

Qua Jun 16, 2010 21:39
Progressões
-
- EXPRESSAO
 por JOHNY » Dom Set 05, 2010 15:26
por JOHNY » Dom Set 05, 2010 15:26
- 1 Respostas
- 2086 Exibições
- Última mensagem por MarceloFantini

Seg Set 06, 2010 13:14
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\[\frac{49^-^6.343^-^3}{(7^2)^-^3.\frac{1}{7}^-^7}\] \[\frac{49^-^6.343^-^3}{(7^2)^-^3.\frac{1}{7}^-^7}\]](/latexrender/pictures/d57f4846c4579330e11f282084129c98.png)
![\[7^-^8\] \[7^-^8\]](/latexrender/pictures/75fa207eee8580e5aaae3ebf07cba495.png)
![\[7^-^2^2\] \[7^-^2^2\]](/latexrender/pictures/94913510da28c8f30216a44499b36d50.png)
![\[\frac{(7^2)^-^6.(7^3)^-^3}{(7^2)^-^3.7^7} = \frac{7^-^1^2.7^-^9}{7^-^6.7^7} = \frac{7^-^2^1}{7^1} = 7^-^2^1^-^(^+^1^)=7^2^2\] \[\frac{(7^2)^-^6.(7^3)^-^3}{(7^2)^-^3.7^7} = \frac{7^-^1^2.7^-^9}{7^-^6.7^7} = \frac{7^-^2^1}{7^1} = 7^-^2^1^-^(^+^1^)=7^2^2\]](/latexrender/pictures/127c618ce2352602a64cd10a06f53e56.png)

![\[\frac{49^-^6.343^-^3}{(7^2)^-^3.\frac{1}{7}^-^7}\] \[\frac{49^-^6.343^-^3}{(7^2)^-^3.\frac{1}{7}^-^7}\]](/latexrender/pictures/d57f4846c4579330e11f282084129c98.png)
![\[7^-^8\] \[7^-^8\]](/latexrender/pictures/75fa207eee8580e5aaae3ebf07cba495.png)
![\[7^-^2^2\] \[7^-^2^2\]](/latexrender/pictures/94913510da28c8f30216a44499b36d50.png)
![\[\frac{(7^2)^-^6.(7^3)^-^3}{(7^2)^-^3.7^7} = \frac{7^-^1^2.7^-^9}{7^-^6.7^7} = \frac{7^-^2^1}{7^1} = 7^-^2^1^-^(^+^1^)=7^2^2\] \[\frac{(7^2)^-^6.(7^3)^-^3}{(7^2)^-^3.7^7} = \frac{7^-^1^2.7^-^9}{7^-^6.7^7} = \frac{7^-^2^1}{7^1} = 7^-^2^1^-^(^+^1^)=7^2^2\]](/latexrender/pictures/127c618ce2352602a64cd10a06f53e56.png)

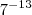 . Daí, suponho que não seja um sétimo elevado a -7, mas
. Daí, suponho que não seja um sétimo elevado a -7, mas 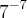

. Daí, suponho que não seja um sétimo elevado a -7, mas
![\[\frac{1}{7}^-^7\] \[\frac{1}{7}^-^7\]](/latexrender/pictures/f7c8bf703481ccf8bc3097f121d6f660.png) e não
e não ![\[7^-^7\] \[7^-^7\]](/latexrender/pictures/6ff979f4933e6554c2809f4c41bdcc63.png)

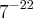



![\[\left ( \frac{1}{7} \right )^-^7 = \frac{7}{7}\] \[\left ( \frac{1}{7} \right )^-^7 = \frac{7}{7}\]](/latexrender/pictures/c2a948702f5cecf47df70a89e938b915.png) e que
e que ![\[\frac{1^(^-^7^)}{7}= \frac{1}{7}\] \[\frac{1^(^-^7^)}{7}= \frac{1}{7}\]](/latexrender/pictures/096c7c7a5b27ae0941cf8c5dd31f3d05.png)
![\[\left ( \frac{1}{7} \right )^-^7 = \left (\frac{7}{1}\right )^7\] \[\left ( \frac{1}{7} \right )^-^7 = \left (\frac{7}{1}\right )^7\]](/latexrender/pictures/93c63c1cc09ebb5ac7bfff7047344f78.png) e que
e que ![\[\frac{1^(^-^7^)}{7}= -\frac{1}{7}\] \[\frac{1^(^-^7^)}{7}= -\frac{1}{7}\]](/latexrender/pictures/4e18aaed643018f978a2586e3547cda6.png)


![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.