Sou do primeiro período de análise de sistemas da metodista de minas, estou tentando resolver uma questão e gostaria da ajuda de vocês, o enunciado é:
Um lote de peçasserá aceito se, tiradas 4 peças ao acaso, forem todas perfeitas. Pergunta-se: que risco corre o fabricante de ter um lote recusado, se ele sabe que 10% das peças que produz são defeituosas? Caso o número de peças tiradas ao acaso seja 2, qual seria o resultado?
Tentei resolver da seguinte forma:
se retirar 4:
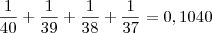que é 10,4%se retirar 2:
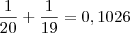que é 10,26%Existe alguma outra forma de fazer ou está correto dessa maneira? Alguém pode me instruir? Não busco nada pronto, quero acompanhamento mesmo...
Desde já agradeço.
por ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)