 por CarinafILIPA » Sex Fev 28, 2014 19:08
por CarinafILIPA » Sex Fev 28, 2014 19:08
Olá bom dia.
Eu tentei resolver as seguintes equações e não consigo, será que me podem ajudar?

a primeira tentei resolver por uma mudança de variável para usar o limite notável
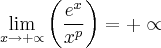
a segunda pensei numa mudança de variavel também no limite notável

não consegui resolver.
-
CarinafILIPA
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Fev 28, 2014 18:44
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por CarinafILIPA » Sáb Mar 01, 2014 12:46
por CarinafILIPA » Sáb Mar 01, 2014 12:46
Será que a resolução da primeira não é assim ?

-
CarinafILIPA
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Fev 28, 2014 18:44
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limites] Exercício com limites notáveis
por fff » Sáb Fev 08, 2014 21:41
- 3 Respostas
- 2672 Exibições
- Última mensagem por e8group

Dom Fev 09, 2014 15:29
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Calcular 2 limites notáveis
por fff » Sex Abr 11, 2014 14:26
- 4 Respostas
- 2515 Exibições
- Última mensagem por fff

Sex Abr 11, 2014 19:12
Cálculo: Limites, Derivadas e Integrais
-
- Limites Notáveis
por spoof » Qui Out 14, 2010 11:23
- 2 Respostas
- 5252 Exibições
- Última mensagem por spoof

Sex Out 15, 2010 14:20
Cálculo: Limites, Derivadas e Integrais
-
- Limites notáveis
por anamendes » Sáb Abr 28, 2012 08:06
- 2 Respostas
- 2088 Exibições
- Última mensagem por anamendes

Sáb Abr 28, 2012 11:15
Cálculo: Limites, Derivadas e Integrais
-
- [limites notáveis]exercício
por fff » Seg Fev 10, 2014 19:35
- 2 Respostas
- 1741 Exibições
- Última mensagem por fff

Ter Fev 11, 2014 14:57
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

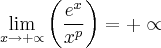






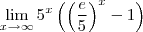


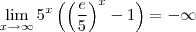

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.