Preciso de ajuda para entender (como se resolve) a seguinte questão de PG!
(U.F.PE) Seja
 um quadrado de lado medindo
um quadrado de lado medindo 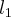 unidades de comprimento. Unindo-se os pontos médios dos lados de
unidades de comprimento. Unindo-se os pontos médios dos lados de  , formamos um novo quadrado
, formamos um novo quadrado 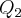 de lado medindo
de lado medindo  unidades de comprimento. Assim procedendo indefinidamente, obtemos a sequência de quadrados
unidades de comprimento. Assim procedendo indefinidamente, obtemos a sequência de quadrados  , onde
, onde 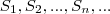 são, respectivamente, as medidas das áreas destes quadrados. Assinale a alternativa que corresponde à soma
são, respectivamente, as medidas das áreas destes quadrados. Assinale a alternativa que corresponde à soma 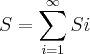
a)
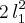 unidades de comprimento
unidades de comprimentob)
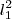 unidades de comprimento
unidades de comprimentoc)
 unidades de comprimento
unidades de comprimentod) (
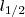 )² unidades de comprimento
)² unidades de comprimentoe)
 unidades de comprimento
unidades de comprimento***Gabarito: a
Obrigada a todos!


 para contar os sucessivos quadrados obtidos sendo
para contar os sucessivos quadrados obtidos sendo  o primeiro, temos a seguinte relação de recorrência:
o primeiro, temos a seguinte relação de recorrência: 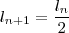
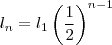 .
. do
do  -ésimo quadrado é dada pelo quadrado da medida de seu lado.
-ésimo quadrado é dada pelo quadrado da medida de seu lado. 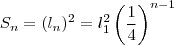
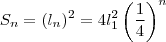 .
.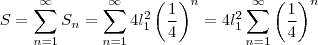
 . É conhecido que
. É conhecido que 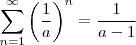 se
se  .
.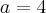 , então
, então 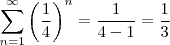 . Daí,
. Daí, 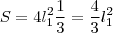 .
.
 .
.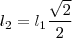
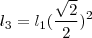

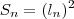 , temos que cada quadrado terá área
, temos que cada quadrado terá área 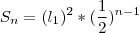 , logo,
, logo,
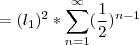 , observe que temos ao lado a soma de uma p.g. de termo inicial 1 e razão 1/2 .
, observe que temos ao lado a soma de uma p.g. de termo inicial 1 e razão 1/2 .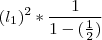
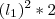

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)