 por Laio » Ter Fev 25, 2014 22:22
por Laio » Ter Fev 25, 2014 22:22
Travei aqui na solução deste logaritmo. Não sei o que posso fazer com essa divisão de logaritmos de mesma base. Ajuuuuuuda!

Como continuo?
-
Laio
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Fev 15, 2014 19:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Eletrônica
- Andamento: formado
 por young_jedi » Ter Fev 25, 2014 22:52
por young_jedi » Ter Fev 25, 2014 22:52
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Laio » Qua Fev 26, 2014 09:37
por Laio » Qua Fev 26, 2014 09:37
Legal, usando Báskara, as raízes serão -3 e +9, mas apenas -3 satisfaz a condição de existência do logaritmo. Resposta:V={-3} OBRIGADO!

Mas este exercício me fez pensar em outra dúvida que eu tinha:
Quando eu tenho uma equação de segundo grau tal como essa à qual você chegou, x²-6x-27=0, eu poderia muito bem passar toda a expressão para o outro lado da igualdade e inverter o sinal de todo mundo, ficando 0=-x²+6x+27. Já testei o cálculo e comprovei que isso obviamente não altera o resultado. Mas se me pedissem para desenhar um gráfico com a parábola dessa equação, no primeiro caso eu veria que a>0 e faria uma parábola aberta para cima. No segundo caso, uma parábola aberta para baixo, pois a<0. Mas isso não é possível, pois se trata da mesma equação! O que é que está errado no meu raciocínio?
-
Laio
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Fev 15, 2014 19:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Eletrônica
- Andamento: formado
 por young_jedi » Qua Fev 26, 2014 16:36
por young_jedi » Qua Fev 26, 2014 16:36
Seu raciocinio esta correto, note que em um primeiro momento a função que você teria é esta
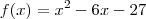
e a outra função seria

são duas funções diferentes, mas que possuem as mesmas raizes, agora quando se fala em equação somente
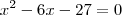
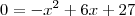
temos que essas duas equações são a mesma coisa ou seja são a mesma equação
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Laio » Qua Fev 26, 2014 17:13
por Laio » Qua Fev 26, 2014 17:13
Tá certo. O sinal só é sagrado se a equação de segundo grau for uma função no plano cartesiano. Agradeço de novo, Skywalker!
-
Laio
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Fev 15, 2014 19:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Eletrônica
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- logaritmos - mudança de base
por Raquel » Seg Mar 29, 2010 20:02
- 2 Respostas
- 7277 Exibições
- Última mensagem por rodrigorfg

Sáb Abr 10, 2010 01:26
Logaritmos
-
- logaritmos com mudançã de base
por cristina » Ter Jun 08, 2010 10:23
- 4 Respostas
- 2351 Exibições
- Última mensagem por cristina

Ter Jun 08, 2010 11:38
Logaritmos
-
- [Logaritmos] Mudança de Base
por b_afa » Seg Nov 18, 2013 19:29
- 1 Respostas
- 1607 Exibições
- Última mensagem por DanielFerreira

Seg Fev 17, 2014 15:22
Logaritmos
-
- Explicação sobre como resolver logaritmos naturais (base e)
por samra » Sáb Mar 24, 2012 12:06
- 3 Respostas
- 4734 Exibições
- Última mensagem por samra

Sáb Mar 24, 2012 23:21
Logaritmos
-
- Função Composta por si mesma
 por WMayalah » Sáb Ago 27, 2011 00:30
por WMayalah » Sáb Ago 27, 2011 00:30
- 1 Respostas
- 1119 Exibições
- Última mensagem por LuizAquino

Sáb Ago 27, 2011 13:01
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




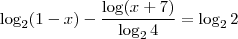
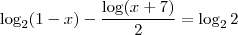
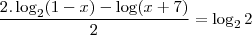
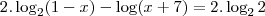
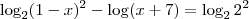
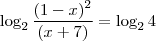
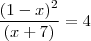
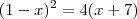
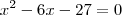



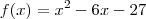

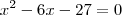
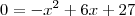


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
