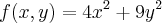 para
para  ;
;  ;
;  e
e 
O meu problema é resolver esse tipo de função atribuindo os valores de
 pelo simples motivo:
pelo simples motivo:Uma dica que essa questão me deu é que essa função representa uma elipse, mas eu não enxerguei isso.
Eu tentei verificar se essa função é ou não uma elipse completando quadrados. Então seria mais ou menos assim:
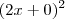 para o
para o  e
e 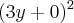 para
para  , centro na origem.
, centro na origem.E na hora de comparar essa função, atribuindo para c = 2, por exemplo, eu dividi toda a equação por 2, e olha o que aconteceu:
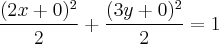
Os semi-eixos maior e menor são iguais, então não poderia ser uma elipse, e sim uma circunferência, pois os raios são iguais.
Será que tem alguma alternativa que demonstra que essa equação realmente é de uma elipse?
Bom, espero que tenham compreendido a minha dúvida e obrigado para quem pôde me ajudar.

Abraço!




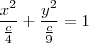

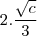


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  .
.