Olá! Estou estudando física, e estava indo tudo bem, até aparecer uma questão envolvendo uma função. Na verdade, a minha maior dificuldade é para simplificar, eu realmente não sei.
A questão para se basear é:
e= 2t² - 1
E pede pra encontrar a função horária da velocidade escalar média entre t' e t, que fica:
Vm=
e'-e
___
t'-t
(2t'²-1)-(2t²-1)
_____________
t'-t
2t'²-2t²
______
t'-t
2(t'+t)(t'-t)
_________
t'-t
Vm= 2(t'+t)
Essa questão, mais ou menos, deu pra eu entender. Mas a questão seguinte, sem resolução, não consigo resolver de jeito nenhum, faz dois dias que estou tentando, e as coisas não se encaixam na minha mente... É a seguinte:
Encontrar a função horária da velocidade escalar média, a partir da seguinte função:
e= 4t² -2t
Me ajudem, por favor, nem que seja me indicando um bom livro de matemática. Preciso entender tudo de física e matemática até agosto, sei que errei ao começar a estudar física ao invés de matemática, mas eu necessito compreender essa questão em especial, se não eu não sossego, questão de honra! Agradeço desde já!


 entre dois instantes de tempo
entre dois instantes de tempo 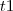 e
e  é definida por
é definida por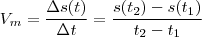
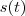 é a posição do móvel no instante
é a posição do móvel no instante  .
.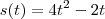 , então
, então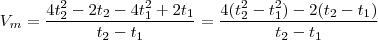
 e
e  reais vale
reais vale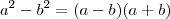 .
.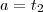 e
e 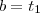 . Assim,
. Assim, 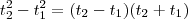
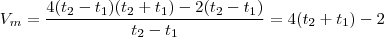
 .
.


 .
.
 :
: