Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por DanielFerreira » Sáb Set 08, 2012 21:39
por DanielFerreira » Sáb Set 08, 2012 21:39
A soma das idades atuais de Maria e Ana é 44 anos. Atualmente, a idade de Maria é o dobro da idade que Ana tinha quando Maria tinha a metade da idade que Ana terá quando a idade desta for o triplo da idade que Maria tinha quando Maria tinha o triplo da idade de Ana. Com base nessas informações calcule a idade de Ana.
Resp.: 16 anos 6 meses.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por young_jedi » Seg Set 10, 2012 16:29
por young_jedi » Seg Set 10, 2012 16:29
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por DanielFerreira » Seg Set 10, 2012 23:33
por DanielFerreira » Seg Set 10, 2012 23:33
Young_jedi,
boa noite!
Devo confessar que se tivesse tentado fazer como você fez, não chegaria num resultado satisfatório. Segue a forma como fiz:
Maria tem:
xAna tem:
yMaria tinha:
x - aAna tinha:
y - aMaria terá:
x + bAna terá:
y + bCONDIÇÃO I:
danjr5 escreveu:A soma das idades atuais de Maria e Ana é 44...
 CONDIÇÃO II
CONDIÇÃO II:
danjr5 escreveu:Atualmente a idade de Maria é o dobro da idade que Ana tinha...
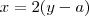 CONDIÇÃO III
CONDIÇÃO III:
danjr5 escreveu:... Maria tinha a metade da idade que Ana terá...
 CONDIÇÃO IV
CONDIÇÃO IV:
danjr5 escreveu:... a idade desta (Ana) for o triplo da idade que Maria tinha...
 CONDIÇÃO V
CONDIÇÃO V:
danjr5 escreveu:... Maria tinha o triplo da idade de Ana.

- Devemos isolar
a e
b;
e,
- Substituir, sucessivamente, a última equação/condição na 'antecessora'.
Isolando
a da
CONDIÇÃO V teremos
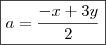
; Substituindo-a na
CONDIÇÃO IV, resulta

Substituindo

na
CONDIÇÃO III, teremos

E finalmente, substituindo

na
CONDIÇÃO II, teremos
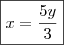
Agora...

Resolvendo-o...
y = 16 anos 6 mesesAté logo.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por young_jedi » Seg Set 10, 2012 23:48
por young_jedi » Seg Set 10, 2012 23:48
danjr5
A grande sacada do exercicio realmente é separar ele em condições, eu parti da ultima condição e fui voltando ate a primeira, ja voce equacionou cada condição separadamente e depois fez um sistema de equações pra chegar ate a resposta, bacana. Valeu ai ate mais
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por tenebroso » Qua Dez 18, 2013 16:34
por tenebroso » Qua Dez 18, 2013 16:34
quando eu chego até esse nível?
-
tenebroso
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Dez 18, 2013 16:00
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: estudante
- Andamento: cursando
 por tenebroso » Qua Dez 18, 2013 16:40
por tenebroso » Qua Dez 18, 2013 16:40
O lucro obtido por um comerciante na venda de determinado produto é dado , em reais, pela função L(x)= -1/10x²+ 15x, sendo x o número de unidades vendidas e o menor que x menor que 150.
Se L(m) é o lucro máximo que comerciante tem condições de obter, pode-se afirmar que log( l(m)/3m) é igual a:
a) 1+2log2
b) 2log2+log5
c) 2-log5 QUEM CONSEGUE RESOLVER? EU NÃO CONSEGUI, ALGUÉM CONSEGUE?
d) 1-2log2
e) 1-2log5
-
tenebroso
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Dez 18, 2013 16:00
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: estudante
- Andamento: cursando
 por DanielFerreira » Ter Fev 18, 2014 11:46
por DanielFerreira » Ter Fev 18, 2014 11:46
Olá tenebroso,
abra um tópicos para suas dúvidas!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Desafios Difíceis
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema de idade
por Alessandra Cezario » Qua Abr 20, 2011 12:57
- 4 Respostas
- 5810 Exibições
- Última mensagem por LuizAquino

Dom Abr 24, 2011 20:12
Problemas do Cotidiano
-
- problema para calcular idade
por Angela Pimenta » Qui Out 27, 2011 14:44
- 3 Respostas
- 2922 Exibições
- Última mensagem por Angela Pimenta

Seg Out 31, 2011 18:18
Funções
-
- Idade
por Ananda » Qua Fev 27, 2008 16:18
- 3 Respostas
- 3453 Exibições
- Última mensagem por admin

Qua Fev 27, 2008 18:21
Problemas do Cotidiano
-
- Idade!
por geriane » Seg Abr 05, 2010 10:49
- 3 Respostas
- 5064 Exibições
- Última mensagem por geriane

Seg Abr 05, 2010 23:57
Desafios Fáceis
-
- Idade do escritor
por Cleyson007 » Qua Jun 10, 2009 09:47
- 6 Respostas
- 3754 Exibições
- Última mensagem por ginrj

Qua Jun 10, 2009 18:04
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


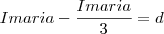

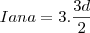

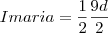
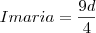
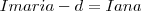
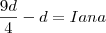







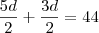


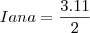



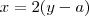



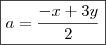 ; Substituindo-a na
; Substituindo-a na 

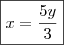



![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.