 por IlgssonBraga » Sáb Fev 08, 2014 17:32
por IlgssonBraga » Sáb Fev 08, 2014 17:32
Bem pessoal, eu queria saber se para provar que o limite de uma função é um determinado L pela definição formal eu posso provar separadamente cada parte dessa função usando as propriedades operatórias de um limite (devidamente comprovadas).
Exemplo: Prove que
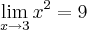
.
Aí eu poderia fazer (nesse caso aqui assumindo como verdadeira a operação de multiplicação de limites)
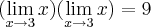
Como,
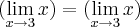
Intuitivamente temos:

Agora provar isso:
Para todo

existe um
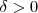
tal que
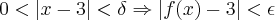
Fazendo nesse caso

temos que é verdadeiro que

Agora substituindo lá em cima:
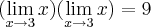
3.3=9
9=9 (C.Q.D)
Fica demonstrado, só não sei se é um jeito correto. Alguém pode me dizer se pode ser feito assim ?
-
IlgssonBraga
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Jul 18, 2013 10:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
 por e8group » Sáb Fev 08, 2014 19:51
por e8group » Sáb Fev 08, 2014 19:51
Na minha opinião, o que fez foi provar que o limite da função identidade existe .Mas isto não prova que o limite da função (definida por

) existe .
Comentário :
Considere
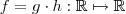
e suponha que demonstramos que os limites
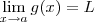
e
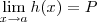
existem, ou seja , mostramos que
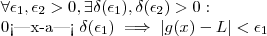
e
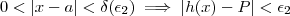
.
Agora ,imaginemos que queremos demonstrar
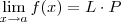
.Isto é, queremos mostrar que dado

existe

tal que se

então

.
A ideia é mostrar que existe

(e este número pode ter alguma relação com os
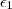
e
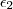
) e em seguida obter

correspondente .
Mas se tomarmos
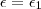
ou
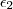
,não necessariamente garantimos que o limite de

é
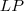
quando

tende a

.
Vamos ao caso em que
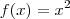
.
Para
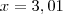
. Tomando-se
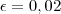
, obtemos
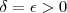
tal que
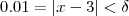
. Mas por outro lado ,
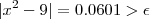
.
Neste link
http://math.berkeley.edu/~drizzolo/Math ... proofs.pdf há uma demostração .
Este exemplo me despertou curiosidade e tentar demonstrar
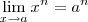
(n natural)
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por IlgssonBraga » Qua Fev 12, 2014 14:53
por IlgssonBraga » Qua Fev 12, 2014 14:53
Não sei se foi isso que vc quis mostrar, mas eu estava assumindo como verdadeira a propriedade da multiplicação, ou seja, eu iria demonstrá-la para depois usá-la. Feito isso queria saber se o que eu fiz procede. Se eu entendi errado me desculpe!
-
IlgssonBraga
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Jul 18, 2013 10:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
 por e8group » Qua Fev 12, 2014 21:08
por e8group » Qua Fev 12, 2014 21:08
Sim , compreendo que fez hipótese da multiplicação . Estou percebendo que provar a regra operatória "limite do produto é produto dos limites" via definição rigorosa de limite é um pouco complicado. Pesquisando em inglês "How can I prove the product rule of limits? " encontrei o site abaixo
http://planetmath.org/proofoflimitruleofproduct que apresenta uma demonstração . Acho que devemos sim utilizar as proposições , regras operatórias a favor de facilitar a demonstração ,há casos realmente medonho de encontra o epsilon's e os delta's correspondentes.Mas no meu ponto de vista este não é o caso .Quando estamos trabalhando com funções

definida pelo monômio

, podemos provar
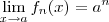
, sem a regra operatória já mencionada.Pq não tentar ? O que acha ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por IlgssonBraga » Qua Fev 12, 2014 22:48
por IlgssonBraga » Qua Fev 12, 2014 22:48
Blz, então me responde só mais essa. Vi isso em algum lugar.
Prove que
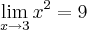
.
Solução:
Para todo

existe um
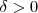
tal que:
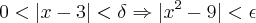
E como
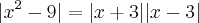

Daí como |x+3|>0 então
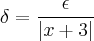
Para esse

>0 existe um
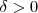
portanto o limite existe
Desse jeito pode ser ?
-
IlgssonBraga
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Jul 18, 2013 10:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
 por e8group » Qui Fev 13, 2014 19:45
por e8group » Qui Fev 13, 2014 19:45
Na minha opinião está certo , e assim o delta dependerá de

(dado) e

. Agora só para complementar... como estamos trabalhando com

próximo de

, pondo

e escolhendo
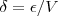
,teremos
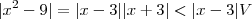
.Daí, se
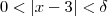
então
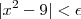
.
Agora q vou postar adiante é de leitura opcional .
E quando
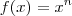
p/ algum

natural . Como provar que
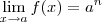
para qq . a real ?? Está tentei fazer , e observei q dado

e tomando-se
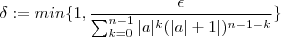
, então se

logo

.Quando fazermos

e

o delta será igual ao menor valor do conjunto
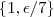
.
Do caso geral ao particular , veja a solução proposta do primeiro link que postei
http://math.berkeley.edu/~drizzolo/Math ... proofs.pdf ,
conforme o link acima podemos ver que o delta é o menor valor entre 1 e epsilon dividido por 7 , ou seja , a mesma escolha do delta do caso geral com n= 2 e a = 3 .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limites] Limites no "infinito " prova a existência ......
por e8group » Dom Jun 17, 2012 14:37
- 2 Respostas
- 2749 Exibições
- Última mensagem por e8group

Ter Jun 19, 2012 11:20
Cálculo: Limites, Derivadas e Integrais
-
- Limites - erro em prova?
 por LFurriel » Dom Jul 25, 2010 22:41
por LFurriel » Dom Jul 25, 2010 22:41
- 5 Respostas
- 3595 Exibições
- Última mensagem por MarceloFantini

Seg Jul 26, 2010 15:28
Cálculo: Limites, Derivadas e Integrais
-
- [teoria de limites] dúvida numa questão de prova
por Fabio Wanderley » Sex Abr 13, 2012 23:38
- 2 Respostas
- 1945 Exibições
- Última mensagem por Fabio Wanderley

Sáb Abr 14, 2012 00:43
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] duas variáveis. Prova através da definição formal
por marcosmuscul » Sáb Jan 25, 2014 17:59
- 2 Respostas
- 6101 Exibições
- Última mensagem por marcosmuscul

Ter Fev 04, 2014 10:03
Cálculo: Limites, Derivadas e Integrais
-
- [limites] reciso de ajuda nessa questão de limites raiz quad
por alexia » Ter Nov 15, 2011 19:55
- 1 Respostas
- 5406 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:16
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
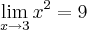 .
.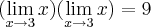
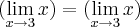

 existe um
existe um 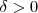 tal que
tal que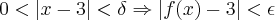
 temos que é verdadeiro que
temos que é verdadeiro que 
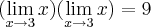


 ) existe .
) existe . 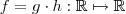 e suponha que demonstramos que os limites
e suponha que demonstramos que os limites 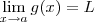 e
e 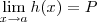 existem, ou seja , mostramos que
existem, ou seja , mostramos que 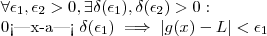
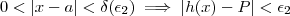 .
. 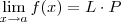 .Isto é, queremos mostrar que dado
.Isto é, queremos mostrar que dado  existe
existe  tal que se
tal que se  então
então  .
.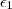 e
e 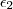 ) e em seguida obter
) e em seguida obter  correspondente .
correspondente . 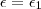 ou
ou  é
é 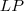 quando
quando  tende a
tende a  .
. 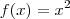 .
. 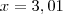 . Tomando-se
. Tomando-se 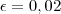 , obtemos
, obtemos 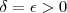 tal que
tal que 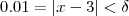 . Mas por outro lado ,
. Mas por outro lado , 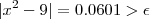 .
. 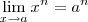 (n natural)
(n natural)
 definida pelo monômio
definida pelo monômio  , podemos provar
, podemos provar 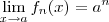 , sem a regra operatória já mencionada.Pq não tentar ? O que acha ?
, sem a regra operatória já mencionada.Pq não tentar ? O que acha ?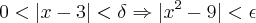
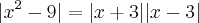

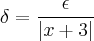
 >0 existe um
>0 existe um  , pondo
, pondo  e escolhendo
e escolhendo 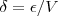 ,teremos
,teremos 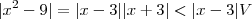 .Daí, se
.Daí, se 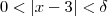 então
então 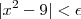 .
.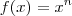 p/ algum
p/ algum  natural . Como provar que
natural . Como provar que 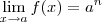 para qq . a real ?? Está tentei fazer , e observei q dado
para qq . a real ?? Está tentei fazer , e observei q dado 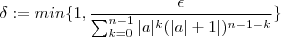 , então se
, então se  logo
logo  .Quando fazermos
.Quando fazermos  e
e  o delta será igual ao menor valor do conjunto
o delta será igual ao menor valor do conjunto 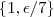 .
.