 por Questioner » Dom Mai 23, 2010 13:12
por Questioner » Dom Mai 23, 2010 13:12
Olá,
Preciso determinar se a seguinte série converge:
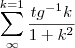
Comecei utilizando o teste da integral:
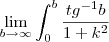
Ok. Observando, lembrei que se utiliza-se a ideia de que:
![\int_{}^{} \frac{dx}{\sqrt[]{1+{x}^{2}}} \int_{}^{} \frac{dx}{\sqrt[]{1+{x}^{2}}}](/latexrender/pictures/29bee737b38bc71589ef2c8c8999443e.png)
e nela podemos usar uma substituição trigonométrica.
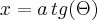
Ou seja, a equação poderia ser descrita como:
} \lim_{b\rightarrow\infty} \int_{0}^{b} \frac{{tg}^{-1} b}{\sqrt[]({}1+{b}^{4})}](/latexrender/pictures/89ae8a6102996430f0724d5bf0ccad0a.png)
Substituindo:
![{x}^{2} = tg(\Theta)\, ,x = \sqrt[]{tg(\Theta)}\, ,d({x}^{2}) = {sec}^{2}(\Theta) {x}^{2} = tg(\Theta)\, ,x = \sqrt[]{tg(\Theta)}\, ,d({x}^{2}) = {sec}^{2}(\Theta)](/latexrender/pictures/d82b05acd82cb77f630e197f5886e93d.png)
Ou seja,
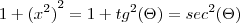 ATENÇÃO AGORA
ATENÇÃO AGORA. Fiz de dois jeitos distintos, pois fiquei na dúvida. Vejam se algum confere, por favor:
JEITO AVoltando a primeira integral:

Seguindo:
![\int_{}^{} arctg(\Theta)= arccotg (\Theta) + ln\,\sqrt[]{2} + C \int_{}^{} arctg(\Theta)= arccotg (\Theta) + ln\,\sqrt[]{2} + C](/latexrender/pictures/32a6d0a1b1e2038805a8d6198d85f969.png)
Limite:
![\lim_{b\rightarrow\infty} arccotg (b) + ln\,\sqrt[]{2} \lim_{b\rightarrow\infty} arccotg (b) + ln\,\sqrt[]{2}](/latexrender/pictures/516ab18989298efec4ad2a8345511fa3.png)
O jeito B também não confere com o resultado final.
RESULTADO FINAL: 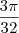
Acho que fiz uma tempestade em um copo d'água. A resolução deve ser muito mais simples, mas não consigo vê-la. Alguém pode me ajudar?
Obrigado!
-
Questioner
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Abr 20, 2010 22:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por magellanicLMC » Qua Fev 05, 2014 22:06
por magellanicLMC » Qua Fev 05, 2014 22:06
está certo o teste que tu resolveu usar mas primeiro tu pode facilitar a questão trazendo p uma função de x que vá se comportar de uma forma já conhecida no caso eu faria
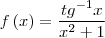
e começaria a trabalhar a partir dela
p/ que o teste da integral seja efetuado precisamos primeiro conferir algumas condições
1) a série ser decrescente e continua
2)apresentar termos positivos p/ x maior que 1
supondo que a função de fato admita essas condições vamos aplicar o teste da integral (caso tu tenhas dificuldades aqui pergunte)
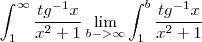
considerando
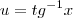
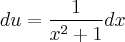
que é exatamente o que temos em nossa integral, substituindo fica
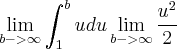
voltando p/u e aplicando os limites fica
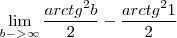
analisando o gráfico da tangente e invertendo nos temos o gráfico da arcotangente ou seja
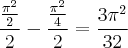
-
magellanicLMC
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Jan 28, 2014 20:35
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Qui Fev 06, 2014 12:21
por e8group » Qui Fev 06, 2014 12:21
Se não foi determinado um método a seguir , no meu ponto de vista , um método bem simples é o dá comparação .
Observe que a função tangente definida do intervalo
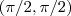
ao

é injetora e sobrejetora (podemos ver esboçando o gráfico) . Assim , a função arco tangente (inversa da tangente) está bem definida de

em
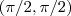
e esta função por sua vez é limitada superiormente por

e inferiormente por

e assim ela é limitada por

o que significa que
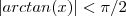
para todo

. Quando multiplicamos está desigualdade por
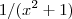
obtemos que
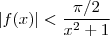
. Desta forma , para

, pondo
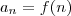
temos
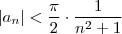
.Pelo que
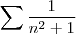
converge ,então
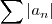
converge .Logo ,

converge .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por magellanicLMC » Qui Fev 06, 2014 23:07
por magellanicLMC » Qui Fev 06, 2014 23:07
concordo com o que tu desenvolveu santhiago, eu realmente só fiz pelo método mais trabalhoso pqe falava em integral no enunciado mas é preferível o teu jeito hahaha
-
magellanicLMC
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Jan 28, 2014 20:35
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [SÉRIE] teste da integral
por magellanicLMC » Qua Fev 05, 2014 20:38
- 1 Respostas
- 1783 Exibições
- Última mensagem por e8group

Qui Fev 06, 2014 11:55
Cálculo: Limites, Derivadas e Integrais
-
- Duvida de Série pelo teste da integral
por douglasnickson » Sáb Ago 20, 2016 13:41
- 0 Respostas
- 4067 Exibições
- Última mensagem por douglasnickson

Sáb Ago 20, 2016 13:41
Sequências
-
- [Série] Calcular valor de série tendo outra como referência
por robmenas » Dom Abr 07, 2019 14:35
- 0 Respostas
- 9182 Exibições
- Última mensagem por robmenas

Dom Abr 07, 2019 14:35
Sequências
-
- [série de Euler / problema da Basiléia] Série de Fourier
por Burnys » Qua Jul 16, 2008 14:34
- 4 Respostas
- 9072 Exibições
- Última mensagem por admin

Qui Jul 17, 2008 00:33
Sequências
-
- Série
por jccp » Seg Dez 16, 2013 01:44
- 3 Respostas
- 2695 Exibições
- Última mensagem por Russman

Seg Dez 16, 2013 20:19
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
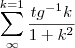
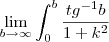
![\int_{}^{} \frac{dx}{\sqrt[]{1+{x}^{2}}} \int_{}^{} \frac{dx}{\sqrt[]{1+{x}^{2}}}](/latexrender/pictures/29bee737b38bc71589ef2c8c8999443e.png)
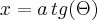
} \lim_{b\rightarrow\infty} \int_{0}^{b} \frac{{tg}^{-1} b}{\sqrt[]({}1+{b}^{4})}](/latexrender/pictures/89ae8a6102996430f0724d5bf0ccad0a.png)
![{x}^{2} = tg(\Theta)\, ,x = \sqrt[]{tg(\Theta)}\, ,d({x}^{2}) = {sec}^{2}(\Theta) {x}^{2} = tg(\Theta)\, ,x = \sqrt[]{tg(\Theta)}\, ,d({x}^{2}) = {sec}^{2}(\Theta)](/latexrender/pictures/d82b05acd82cb77f630e197f5886e93d.png)
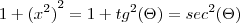

![\int_{}^{} arctg(\Theta)= arccotg (\Theta) + ln\,\sqrt[]{2} + C \int_{}^{} arctg(\Theta)= arccotg (\Theta) + ln\,\sqrt[]{2} + C](/latexrender/pictures/32a6d0a1b1e2038805a8d6198d85f969.png)
![\lim_{b\rightarrow\infty} arccotg (b) + ln\,\sqrt[]{2} \lim_{b\rightarrow\infty} arccotg (b) + ln\,\sqrt[]{2}](/latexrender/pictures/516ab18989298efec4ad2a8345511fa3.png)


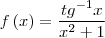 e começaria a trabalhar a partir dela
e começaria a trabalhar a partir dela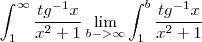
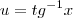
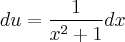 que é exatamente o que temos em nossa integral, substituindo fica
que é exatamente o que temos em nossa integral, substituindo fica 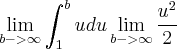 voltando p/u e aplicando os limites fica
voltando p/u e aplicando os limites fica 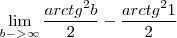
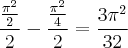

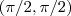 ao
ao  é injetora e sobrejetora (podemos ver esboçando o gráfico) . Assim , a função arco tangente (inversa da tangente) está bem definida de
é injetora e sobrejetora (podemos ver esboçando o gráfico) . Assim , a função arco tangente (inversa da tangente) está bem definida de  e inferiormente por
e inferiormente por  e assim ela é limitada por
e assim ela é limitada por 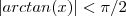 para todo
para todo  . Quando multiplicamos está desigualdade por
. Quando multiplicamos está desigualdade por 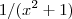 obtemos que
obtemos que 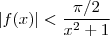 . Desta forma , para
. Desta forma , para  , pondo
, pondo 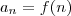 temos
temos 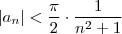 .Pelo que
.Pelo que 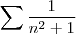 converge ,então
converge ,então 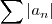 converge .Logo ,
converge .Logo ,  converge .
converge .