 por e8group » Qui Fev 06, 2014 22:16
por e8group » Qui Fev 06, 2014 22:16
Dica :
Faça uma substituição

, logo
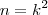
e assim , a desigualdade se escreve como

ou ainda
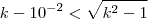
.Pelo que o lado esquerdo da inequação é um número positivo então podemos elevar ambos lados ao quadrado e após simplificações obterá a solução que nos permite analisar o menor natural .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Qui Fev 06, 2014 22:30
por e8group » Qui Fev 06, 2014 22:30
Outra forma é multiplicar a desigualdade por

e utilizar que
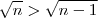
implicando
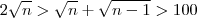
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Inteiro Estritamente Positivo
por gustavowelp » Dom Jun 27, 2010 22:18
- 2 Respostas
- 1757 Exibições
- Última mensagem por gustavowelp

Seg Jun 28, 2010 07:01
Sistemas de Equações
-
- Menor elemento positivo
por Cleyson007 » Sex Abr 13, 2012 22:42
- 0 Respostas
- 682 Exibições
- Última mensagem por Cleyson007

Sex Abr 13, 2012 22:42
Álgebra Elementar
-
- Inequação - 2º grau com delta menor que zero
por renanrdaros » Sex Mar 25, 2011 18:27
- 8 Respostas
- 7430 Exibições
- Última mensagem por johnlaw

Dom Mar 27, 2011 16:33
Álgebra Elementar
-
- Número inteiro
por thadeu » Qua Nov 18, 2009 19:27
- 0 Respostas
- 920 Exibições
- Última mensagem por thadeu

Qua Nov 18, 2009 19:27
Álgebra Elementar
-
- número inteiro 1
por jose henrique » Sáb Fev 12, 2011 16:42
- 4 Respostas
- 2386 Exibições
- Última mensagem por jose henrique

Sáb Fev 12, 2011 20:41
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 tal que
tal que ![\sqrt[2]{n}-\sqrt[2]{n-1}<0,01 \sqrt[2]{n}-\sqrt[2]{n-1}<0,01](/latexrender/pictures/5f359fd367bc02d5367532dcc71f5b4a.png)
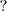

 tal que
tal que ![\sqrt[2]{n}-\sqrt[2]{n-1}<0,01 \sqrt[2]{n}-\sqrt[2]{n-1}<0,01](/latexrender/pictures/5f359fd367bc02d5367532dcc71f5b4a.png)
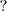

 , logo
, logo 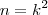 e assim , a desigualdade se escreve como
e assim , a desigualdade se escreve como  ou ainda
ou ainda 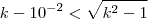 .Pelo que o lado esquerdo da inequação é um número positivo então podemos elevar ambos lados ao quadrado e após simplificações obterá a solução que nos permite analisar o menor natural .
.Pelo que o lado esquerdo da inequação é um número positivo então podemos elevar ambos lados ao quadrado e após simplificações obterá a solução que nos permite analisar o menor natural .
 e utilizar que
e utilizar que 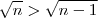 implicando
implicando 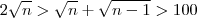 .
.
