
minha dúvida é em relação a qual série eu consigo calcular



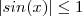 para todo
para todo  e em consequência
e em consequência 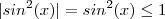 o que implica
o que implica  .Daí vem ,
.Daí vem ,  ... Tente conluir ..
... Tente conluir .. e
e 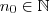 tal que
tal que  ,então a convergência de
,então a convergência de  implica a de
implica a de  .
.
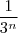 é série geométrica com
é série geométrica com  ela converge, como a superior converge a inferior convergirá também, acredito que esteja certo.
ela converge, como a superior converge a inferior convergirá também, acredito que esteja certo. 
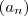 e
e 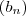 . Faz-se as seguintes hipóteses :
. Faz-se as seguintes hipóteses :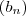 é limitada (convergente ou não)
é limitada (convergente ou não)  é de termos não-negativos .
é de termos não-negativos .  é absolutamente convergente .
é absolutamente convergente .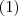 , segue-se que existe
, segue-se que existe  tal que
tal que  para todo
para todo  natural . Multiplicando-se esta desigualdade por
natural . Multiplicando-se esta desigualdade por 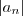 ,temos
,temos 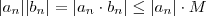 . E assim pela hipótese (2) , obtemos
. E assim pela hipótese (2) , obtemos 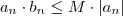 para todo
para todo  e consequentemente ,
e consequentemente , 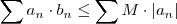 . Daí de (3) resulta (pela proposição postei anteriormente) que a série
. Daí de (3) resulta (pela proposição postei anteriormente) que a série 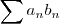 converge .
converge .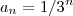 e
e  .As hipóteses (1) ,(2) e (3) são satisfeitas , logo a série de termo geral
.As hipóteses (1) ,(2) e (3) são satisfeitas , logo a série de termo geral  converge .
converge .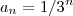 e
e 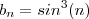 .As hipóteses (1) e (3) são satisfeitas , entretanto a (2) não o é . Porém a série
.As hipóteses (1) e (3) são satisfeitas , entretanto a (2) não o é . Porém a série 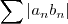 é convergente (porque???) , logo a série
é convergente (porque???) , logo a série 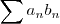 é absolutamente convergente e portanto ela é convergente .
é absolutamente convergente e portanto ela é convergente . 
 ser limitada n implicaria automaticamente que a série da soma de
ser limitada n implicaria automaticamente que a série da soma de  será convergente? tendo um limite superior por exemplo,
será convergente? tendo um limite superior por exemplo, 

magellanicLMC escreveu:n tenho certeza mas na tua primeira condiçãoser limitada n implicaria automaticamente que a série da soma de
será convergente? tendo um limite superior por exemplo,
acho que entendi o que tu disse, basicamente uma relação entre condição e definição, com certeza ajudou
n esperava uma explicação tão detalhada! obrigada novamente.
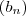 limitada inferiormente por
limitada inferiormente por  e superiormente por
e superiormente por  . Da hipótese , segue
. Da hipótese , segue  para todo
para todo  . Logo o termo geral não és um infinitesimal pelo que a série diverge .
. Logo o termo geral não és um infinitesimal pelo que a série diverge . 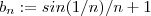 .É claro que (b_n) é limitada , mas seu limite não zero .Logo a série diverge ...
.É claro que (b_n) é limitada , mas seu limite não zero .Logo a série diverge ...
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.