
A 4.1a dá
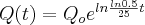 e a 4.1b dá
e a 4.1b dá 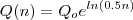 .
.

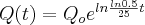 e a 4.1b dá
e a 4.1b dá 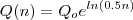 .
.
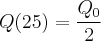 e por outro lado, temos que
e por outro lado, temos que 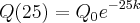 , de modo que ficamos com:
, de modo que ficamos com: , logo a equação modelagem em função de t fica,
, logo a equação modelagem em função de t fica, 
 , agora temos uma função na variável n, logo
, agora temos uma função na variável n, logo 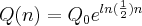 , mas note que
, mas note que , logo minha resposta da b está diferente do seu gabarito o que realmente me deixou inseguro se cometi algum erro (que não consegui encontrar), mas seja como for, acho que a ideia para resolver a questão é essa mesmo.
, logo minha resposta da b está diferente do seu gabarito o que realmente me deixou inseguro se cometi algum erro (que não consegui encontrar), mas seja como for, acho que a ideia para resolver a questão é essa mesmo.


Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

