 .
.Minha resolução:
Consideremos PQ o segmento cuja medida é a amplitude da elipse. Conforme a definição da mesma e o Teorema de Pitágoras, considerando F1 e F2 os focos, temos:

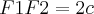

Então:
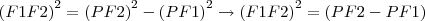
 ---->
---->---->

Porém, pela definição, vem que:

E, aplicando no resultado, temos:
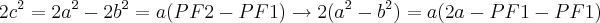
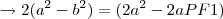

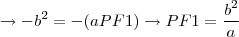
Já tentei resolver outras vezes, mas sempre cheguei no mesmo resultado. Qual é o erro? Por favor, ajudem!
Obrigada!




![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)