 por Isa123 » Dom Dez 29, 2013 21:18
por Isa123 » Dom Dez 29, 2013 21:18
Uma máquina de enchimento automático de garrafas está regulada de tal forma que a quantidade (em centilitros) de vinho vertido para uma garrafa é uma variável aleatória X com distribuição aproximadamente normal de valor médio 78.
O departamento de controlo de qualidade da empresa verificou que, em média, 15,865% das garrafas enchidas pela máquina tinham menos do que os 75 centilitros de vinho indicados no rótulo.
a)Qual é o desvio padrão da variável aleatória X ?
b)Em nome da sua boa imagem, a empresa quer diminuir drasticamente a percentagem de garrafas com menos de 75 centilitros de vinho. A regulação da máquina de enchimento permite modificar o valor médio da variável aleatória X , mas não permite alterar o seu desvio padrão. Para que novo valor médio deverá ser a máquina regulada, de tal forma que apenas 2,275% das garrafas fiquem com menos de 75 centilitros de vinho?
-
Isa123
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Ter Dez 10, 2013 21:38
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Renato_RJ » Seg Dez 30, 2013 21:31
por Renato_RJ » Seg Dez 30, 2013 21:31
Não sou muito versado em estatística, talvez outro usuário seja melhor indicado, mas vou mostrar o que fiz (mas pode estar errado)....
Bem, sabemos que a média é 78, e 15,865% estão abaixo de 75, então vamos normalizar essa distribuição:
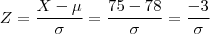
Sabemos que
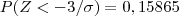
Fazendo
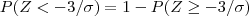
temos que
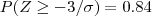
Olhando em uma tabela de distribuição normal, vemos que para a probabilidade de 0.838 ( o mais próximo de 0.84) temos o seguinte valor :
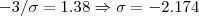
Assim obtemos (espero eu) o valor para o desvio padrão, que é

.
O próximo item é bem semelhante, mas o valor de

é fixado, então cabe achar o valor de

para a probabilidade solicitada.
Espero que alguém mais versado em estatística veja esse tópico e me corrija se estiver errado, pois nunca fui um bom aluno dessa disciplina....
Abraços,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Isa123 » Qui Jan 02, 2014 11:18
por Isa123 » Qui Jan 02, 2014 11:18
Estive a resolver o item seguinte e o X deu me 31,587 está correto?
Muito Obrigado!!
-
Isa123
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Ter Dez 10, 2013 21:38
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Desvio Padrão] Porcentagem do desvio padrão
por GBT » Qui Mar 22, 2012 22:53
- 2 Respostas
- 14642 Exibições
- Última mensagem por fernando7

Dom Mai 13, 2018 21:55
Estatística
-
- Desvio Padrão
 por Cleyson007 » Sáb Jun 13, 2009 11:18
por Cleyson007 » Sáb Jun 13, 2009 11:18
- 1 Respostas
- 4543 Exibições
- Última mensagem por Felipe Schucman

Qua Jul 29, 2009 02:22
Estatística
-
- Desvio padrão
por nina_0 » Dom Mai 08, 2011 19:04
- 1 Respostas
- 3198 Exibições
- Última mensagem por nina_0

Dom Mai 08, 2011 22:20
Estatística
-
- desvio padrao da media (SEM)
por lusasantos » Dom Mai 31, 2009 00:51
- 0 Respostas
- 2850 Exibições
- Última mensagem por lusasantos

Dom Mai 31, 2009 00:51
Estatística
-
- Probabilidade-Desvio Padrão
por veldri » Ter Abr 27, 2010 08:55
- 1 Respostas
- 5316 Exibições
- Última mensagem por Neperiano

Seg Jul 04, 2011 19:42
Dúvidas Pendentes (aguardando novos colaboradores)
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


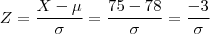
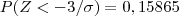
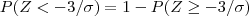 temos que
temos que 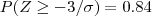
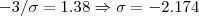
 .
. é fixado, então cabe achar o valor de
é fixado, então cabe achar o valor de  para a probabilidade solicitada.
para a probabilidade solicitada.





