 por mota_16 » Sex Dez 06, 2013 11:12
por mota_16 » Sex Dez 06, 2013 11:12
Pessoal, não consigo resolver essa questão.
As matrizes A, I e J são quadradas de ordem 2 e I é a matriz identidade. Se a matriz A =
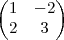
satisfaz as relações
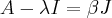
e
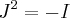
, com

e

números reais, então a matriz J é igual a:
Resposta:
![J=+ ou - \frac{1}{\sqrt[]{3}}
\begin{pmatrix}
-1 & -2 \\
2 & 1
\end{pmatrix} J=+ ou - \frac{1}{\sqrt[]{3}}
\begin{pmatrix}
-1 & -2 \\
2 & 1
\end{pmatrix}](/latexrender/pictures/c62514c673a86917f6b5e6e2ea624f7b.png)
-
mota_16
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Dez 06, 2013 10:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Regular
- Andamento: cursando
 por e8group » Sáb Dez 07, 2013 11:45
por e8group » Sáb Dez 07, 2013 11:45
Uma forma é estabelecer uma relação entre os escaleres
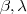
com os termos da matriz inversa de

.Nota a matriz

tem determinante não nulo e assim ela possui inversa e esta matriz denotada por

é única .
Se

então
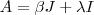
(1) .Multiplicando-se (1) por
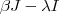
e usando

no lado esquerdo da igualdade e
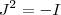
no lado direito ,obtemos
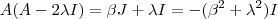
(2) . Logo ,

e assim concluímos que
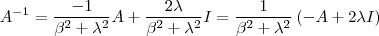
(3) .
Agora tente concluir a parti daí .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por mota_16 » Sáb Dez 07, 2013 19:04
por mota_16 » Sáb Dez 07, 2013 19:04
Olá Santhiago,
Eu consegui entender as passagens, porém ao obter a matriz inversa relacionadas com os escalares eu não tenho mais quem quero descobrir que é exatamente a matriz J. Por isso, não consegui enxergar como a matriz inversa vai me ajudar na resolução do problema. Pensei em fazer
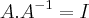
para descobrir os escalares. Como

,

e

, teríamos:
![\begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}
\left[ \frac{1}{{\beta}^{2}+{\lambda}^{2}}\left(-A + 2\lambda I \right) \right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix} \begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}
\left[ \frac{1}{{\beta}^{2}+{\lambda}^{2}}\left(-A + 2\lambda I \right) \right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}](/latexrender/pictures/501f688f5cc5d82b82842ada85d5b873.png)
![\begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}
\left[ \frac{1}{{\beta}^{2}+{\lambda}^{2}}\left(-
\begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}
\right) + 2\lambda I \right) \right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix} \begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}
\left[ \frac{1}{{\beta}^{2}+{\lambda}^{2}}\left(-
\begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}
\right) + 2\lambda I \right) \right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}](/latexrender/pictures/198b718a00ea39b73341b677c16fdf46.png)
![\begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}\left[\frac{1}{{\beta}^{2}+{\lambda}^{2}}\left(
\begin{pmatrix}
-1 & 2 \\
-2 & -3
\end{pmatrix}
\right) +
\begin{pmatrix}
2\lambda & 0 \\
0 & 2\lambda
\end{pmatrix}
\right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix} \begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}\left[\frac{1}{{\beta}^{2}+{\lambda}^{2}}\left(
\begin{pmatrix}
-1 & 2 \\
-2 & -3
\end{pmatrix}
\right) +
\begin{pmatrix}
2\lambda & 0 \\
0 & 2\lambda
\end{pmatrix}
\right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}](/latexrender/pictures/d48f64f33893203438310a00d4527205.png)
![\begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}\left[\frac{1}{{\beta}^{2}+{\lambda}^{2}}
\begin{pmatrix}
2\lambda-1 & 2 \\
-2 & 2\lambda+3
\end{pmatrix}
\right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix} \begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}\left[\frac{1}{{\beta}^{2}+{\lambda}^{2}}
\begin{pmatrix}
2\lambda-1 & 2 \\
-2 & 2\lambda+3
\end{pmatrix}
\right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}](/latexrender/pictures/f970343077885c2f6d6865686bf7bda9.png)
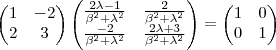
Resolvendo o produto:

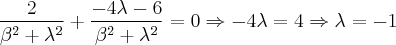
Substituindo na equação anterior, obtém-se
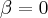
Acho que errei em algum lugar... É esse o raciocínio?
-
mota_16
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Dez 06, 2013 10:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Regular
- Andamento: cursando
 por e8group » Sáb Dez 07, 2013 20:33
por e8group » Sáb Dez 07, 2013 20:33
Parece que você obteve resultado errado devido erros de cálculos . Na verdade sugerir trabalhar com a matriz inversa, por que tem um resultado para matrizes
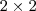
não singulares que nos fornece esta matriz através da aplicação de uma fórmula . (veja :
http://pt.wikipedia.org/wiki/Matriz_inv ... s_2.C3.972) .
Comentário sobre sua resolução :
Na primeira linha após "teríamos " , aquela expressão é equivalente a de baixo
![A\left[ \frac{1}{\beta^2 + \lambda^2}(-A+ 2\lambda I) A\right] = I A\left[ \frac{1}{\beta^2 + \lambda^2}(-A+ 2\lambda I) A\right] = I](/latexrender/pictures/cbc041bc731d574b16f6772bc0ba5e08.png)
que pode ser desenvolvida da seguinte forma :
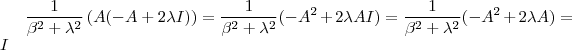
.
Ou ainda ,multiplicando ambos os lados da igualdade por

vamos obter
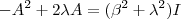
. Como
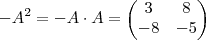
,

e
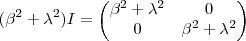
,segue
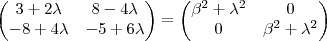
.
Daí , para que esta matrizes sejam iguais teremos
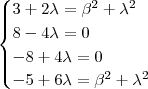
.
De acordo com segunda e terceira equação deste sistema temos
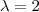
e assim o sistema se reduz a

que nos dá
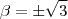
como solução .
Lembrando que

,substituindo os escalares pelos valores encontrados obterá a reposta .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por mota_16 » Sáb Dez 07, 2013 21:00
por mota_16 » Sáb Dez 07, 2013 21:00
santhiago muito obrigado pela ajuda! Entendi perfeitamente como fez! Vou rever meus cálculos e descobrir o erro.
-
mota_16
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Dez 06, 2013 10:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Regular
- Andamento: cursando
 por e8group » Sáb Dez 07, 2013 21:32
por e8group » Sáb Dez 07, 2013 21:32
Há outra forma . Suponha
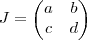
. Pelo que
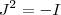
,segue
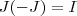
. Portanto

é invertível e sua inversa é

(*)
. Além disso,
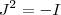
acarreta que
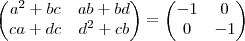
e assim
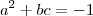
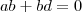


,
equivalentemente ,
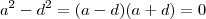

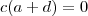
.
Analisando as soluções p/ primeira equação concluímos que

ou

.Se ocorrer

implicará
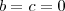
e

.Já na segunda possibilidade , temos
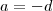
,para este caso devemos encontrar

reais que cumpre
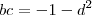
(**) e

(Apenas dividi por \beta e definir os novos escalares como m e p ) . Prosseguindo :
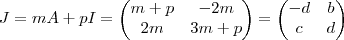
. Logo ,

(1)
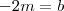
(2)
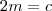
(3)

(4) ,
[(1) +(4)]
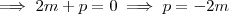
.
Então

. Utilizando estes resultados em (**) ,
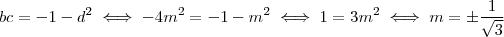
. E assim a,b,c,d estarão bem determinados .
Para aquele primeiro caso em que
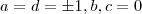
,

se exprimir por
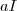
onde

é uma das possibilidades

ou

e assim teremos
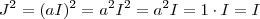
que contradiz o fato de
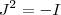
.
Editado .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por mota_16 » Sex Dez 27, 2013 22:06
por mota_16 » Sex Dez 27, 2013 22:06
santhiago, tudo bem?
Estava estudando essa questão novamente e verifiquei que você postou uma nova resolução. E refazendo os passos eu não entendi o por quê do valor do d ser igual a um positivo ou um negativo em "Se ocorrer

implicará
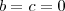
e

". Pode esclarecer?
santhiago escreveu:Há outra forma . Suponha
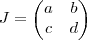
. Pelo que
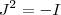
,segue
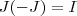
. Portanto

é invertível e sua inversa é

(*)
. Além disso,
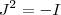
acarreta que
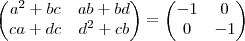
e assim
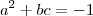
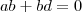


,
equivalentemente ,
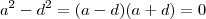

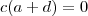
.
Analisando as soluções p/ primeira equação concluímos que

ou

.Se ocorrer

implicará
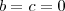
e

.Já na segunda possibilidade , temos
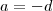
,para este caso devemos encontrar

reais que cumpre
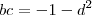
(**) e

(Apenas dividi por \beta e definir os novos escalares como m e p ) . Prosseguindo :
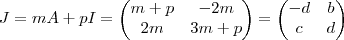
. Logo ,

(1)
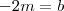
(2)
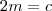
(3)

(4) ,
[(1) +(4)]
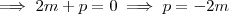
.
Então

. Utilizando estes resultados em (**) ,
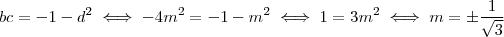
. E assim a,b,c,d estarão bem determinados .
Para aquele primeiro caso em que
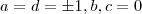
,

se exprimir por
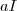
onde

é uma das possibilidades

ou

e assim teremos
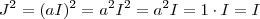
que contradiz o fato de
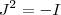
.
Editado .
-
mota_16
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Dez 06, 2013 10:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Regular
- Andamento: cursando
 por e8group » Sex Dez 27, 2013 22:44
por e8group » Sex Dez 27, 2013 22:44
Boa noite . Vou rever a resposta [observei erroneamente a eq
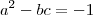
,nesta época que respondi este tópico vi a mesma eq. como
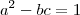
que em consequência nos

se
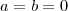
, a seguir vou rever minha resposta ].
Consegue ver que se

então
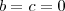
? Caso sim ,note que a matriz

se escreve como
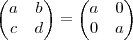
e deixando o número

em evidência ,temos que
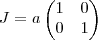
ou de forma mais compacta

.Por hipótese a matriz

é tal que
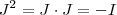
.
Mas, se
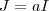
teremos
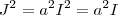
que é um absurdo , pois para qualquer número real

o seu quadrado será positivo e assim vemos que não existe

real p/ o qual
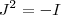
.
Outra forma de notares que

não é real é pela equação que já foi mencionada entre[]
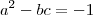
.Com

temos

.
Comente as dúvidas .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por mota_16 » Sex Dez 27, 2013 23:07
por mota_16 » Sex Dez 27, 2013 23:07
Santhiago, perfeito nas explicações!
Entendi perfeitamente o que expôs! A única dúvida era mesmo no valor de d. Muito obrigado!
-
mota_16
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Dez 06, 2013 10:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Regular
- Andamento: cursando
 por mota_16 » Sex Dez 27, 2013 23:45
por mota_16 » Sex Dez 27, 2013 23:45
Santhiago é possível enviar-lhe uma MP (mensagem particular) ? Tentei mas no meu cadastro não estou habilitado. Existe outra forma?
-
mota_16
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Dez 06, 2013 10:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Regular
- Andamento: cursando
 por e8group » Sáb Dez 28, 2013 01:23
por e8group » Sáb Dez 28, 2013 01:23
Boa noite .Possuo o mesmo problema que você (não estou habilitado a enviar MP) .Suponho que somente os moderadores usufruem deste recurso . De qualquer forma, se precisar entrar em contato ,segue-se abaixo meu e-mail
guimaraes_thiago@live.com Att.,
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Identidade Trigonometrica
por MERLAYNE » Ter Abr 24, 2012 19:40
- 4 Respostas
- 2467 Exibições
- Última mensagem por DanielFerreira

Ter Abr 24, 2012 20:12
Trigonometria
-
- Função Identidade
por Jhenrique » Sáb Nov 17, 2012 19:29
- 0 Respostas
- 1280 Exibições
- Última mensagem por Jhenrique

Sáb Nov 17, 2012 19:29
Funções
-
- [Integral] Identidade
por klueger » Seg Mar 04, 2013 17:52
- 1 Respostas
- 1624 Exibições
- Última mensagem por young_jedi

Seg Mar 04, 2013 23:28
Cálculo: Limites, Derivadas e Integrais
-
- [Trigonometria] Identidade trigonometrica
por Alvadorn » Sáb Ago 13, 2011 17:47
- 2 Respostas
- 1892 Exibições
- Última mensagem por Alvadorn

Sáb Ago 13, 2011 20:27
Trigonometria
-
- identidade trigonométrica fundamental
por zenildo » Qui Jun 27, 2013 20:21
- 1 Respostas
- 1484 Exibições
- Última mensagem por young_jedi

Sex Jun 28, 2013 11:22
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
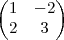 satisfaz as relações
satisfaz as relações 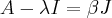 e
e 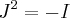 , com
, com  e
e  números reais, então a matriz J é igual a:
números reais, então a matriz J é igual a:![J=+ ou - \frac{1}{\sqrt[]{3}}
\begin{pmatrix}
-1 & -2 \\
2 & 1
\end{pmatrix} J=+ ou - \frac{1}{\sqrt[]{3}}
\begin{pmatrix}
-1 & -2 \\
2 & 1
\end{pmatrix}](/latexrender/pictures/c62514c673a86917f6b5e6e2ea624f7b.png)

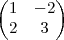 satisfaz as relações
satisfaz as relações 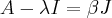 e
e 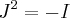 , com
, com  e
e  números reais, então a matriz J é igual a:
números reais, então a matriz J é igual a:![J=+ ou - \frac{1}{\sqrt[]{3}}
\begin{pmatrix}
-1 & -2 \\
2 & 1
\end{pmatrix} J=+ ou - \frac{1}{\sqrt[]{3}}
\begin{pmatrix}
-1 & -2 \\
2 & 1
\end{pmatrix}](/latexrender/pictures/c62514c673a86917f6b5e6e2ea624f7b.png)

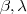 com os termos da matriz inversa de
com os termos da matriz inversa de  .Nota a matriz
.Nota a matriz  tem determinante não nulo e assim ela possui inversa e esta matriz denotada por
tem determinante não nulo e assim ela possui inversa e esta matriz denotada por  é única .
é única .  então
então 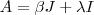 (1) .Multiplicando-se (1) por
(1) .Multiplicando-se (1) por 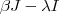 e usando
e usando  no lado esquerdo da igualdade e
no lado esquerdo da igualdade e 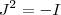 no lado direito ,obtemos
no lado direito ,obtemos 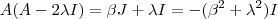 (2) . Logo ,
(2) . Logo ,  e assim concluímos que
e assim concluímos que 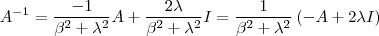 (3) .
(3) .
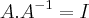 para descobrir os escalares. Como
para descobrir os escalares. Como  ,
,  e
e  , teríamos:
, teríamos:![\begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}
\left[ \frac{1}{{\beta}^{2}+{\lambda}^{2}}\left(-A + 2\lambda I \right) \right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix} \begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}
\left[ \frac{1}{{\beta}^{2}+{\lambda}^{2}}\left(-A + 2\lambda I \right) \right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}](/latexrender/pictures/501f688f5cc5d82b82842ada85d5b873.png)
![\begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}
\left[ \frac{1}{{\beta}^{2}+{\lambda}^{2}}\left(-
\begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}
\right) + 2\lambda I \right) \right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix} \begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}
\left[ \frac{1}{{\beta}^{2}+{\lambda}^{2}}\left(-
\begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}
\right) + 2\lambda I \right) \right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}](/latexrender/pictures/198b718a00ea39b73341b677c16fdf46.png)
![\begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}\left[\frac{1}{{\beta}^{2}+{\lambda}^{2}}\left(
\begin{pmatrix}
-1 & 2 \\
-2 & -3
\end{pmatrix}
\right) +
\begin{pmatrix}
2\lambda & 0 \\
0 & 2\lambda
\end{pmatrix}
\right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix} \begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}\left[\frac{1}{{\beta}^{2}+{\lambda}^{2}}\left(
\begin{pmatrix}
-1 & 2 \\
-2 & -3
\end{pmatrix}
\right) +
\begin{pmatrix}
2\lambda & 0 \\
0 & 2\lambda
\end{pmatrix}
\right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}](/latexrender/pictures/d48f64f33893203438310a00d4527205.png)
![\begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}\left[\frac{1}{{\beta}^{2}+{\lambda}^{2}}
\begin{pmatrix}
2\lambda-1 & 2 \\
-2 & 2\lambda+3
\end{pmatrix}
\right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix} \begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}\left[\frac{1}{{\beta}^{2}+{\lambda}^{2}}
\begin{pmatrix}
2\lambda-1 & 2 \\
-2 & 2\lambda+3
\end{pmatrix}
\right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}](/latexrender/pictures/f970343077885c2f6d6865686bf7bda9.png)
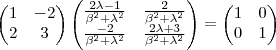

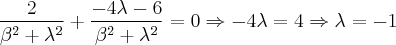
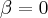

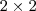 não singulares que nos fornece esta matriz através da aplicação de uma fórmula . (veja : http://pt.wikipedia.org/wiki/Matriz_inv ... s_2.C3.972) .
não singulares que nos fornece esta matriz através da aplicação de uma fórmula . (veja : http://pt.wikipedia.org/wiki/Matriz_inv ... s_2.C3.972) . ![A\left[ \frac{1}{\beta^2 + \lambda^2}(-A+ 2\lambda I) A\right] = I A\left[ \frac{1}{\beta^2 + \lambda^2}(-A+ 2\lambda I) A\right] = I](/latexrender/pictures/cbc041bc731d574b16f6772bc0ba5e08.png) que pode ser desenvolvida da seguinte forma :
que pode ser desenvolvida da seguinte forma : 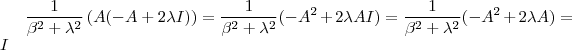 .
.  vamos obter
vamos obter 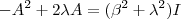 . Como
. Como 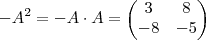 ,
,  e
e 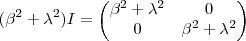 ,segue
,segue 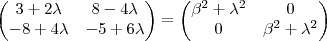 .
. 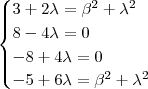 .
. 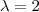 e assim o sistema se reduz a
e assim o sistema se reduz a  que nos dá
que nos dá 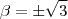 como solução .
como solução .  ,substituindo os escalares pelos valores encontrados obterá a reposta .
,substituindo os escalares pelos valores encontrados obterá a reposta .

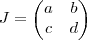 . Pelo que
. Pelo que 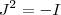 ,segue
,segue 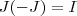 . Portanto
. Portanto  é invertível e sua inversa é
é invertível e sua inversa é  (*)
(*) 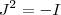 acarreta que
acarreta que 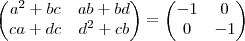 e assim
e assim 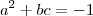
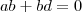

 ,
,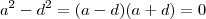

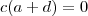 .
.  ou
ou  .Se ocorrer
.Se ocorrer  implicará
implicará 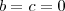 e
e  .Já na segunda possibilidade , temos
.Já na segunda possibilidade , temos 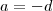 ,para este caso devemos encontrar
,para este caso devemos encontrar  reais que cumpre
reais que cumpre 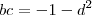 (**) e
(**) e  (Apenas dividi por \beta e definir os novos escalares como m e p ) . Prosseguindo :
(Apenas dividi por \beta e definir os novos escalares como m e p ) . Prosseguindo : 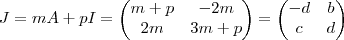 . Logo ,
. Logo ,  (1)
(1)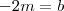 (2)
(2) 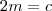 (3)
(3) (4) ,
(4) , 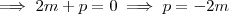 .
.  . Utilizando estes resultados em (**) ,
. Utilizando estes resultados em (**) , 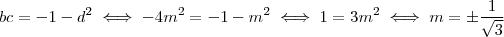 . E assim a,b,c,d estarão bem determinados .
. E assim a,b,c,d estarão bem determinados .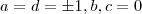 ,
, se exprimir por
se exprimir por 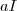 onde
onde  é uma das possibilidades
é uma das possibilidades  ou
ou  e assim teremos
e assim teremos 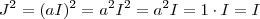 que contradiz o fato de
que contradiz o fato de 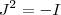 .
. 
 implicará
implicará 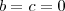 e
e  ". Pode esclarecer?
". Pode esclarecer?. Pelo que
,segue
. Portanto
é invertível e sua inversa é
(*)
acarreta que
e assim
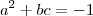
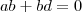

,

.
ou
.Se ocorrer
implicará
e
.Já na segunda possibilidade , temos
,para este caso devemos encontrar
reais que cumpre
(**) e
(Apenas dividi por \beta e definir os novos escalares como m e p ) . Prosseguindo :
. Logo ,
(1)
(2)
(3)
(4) ,
.
. Utilizando estes resultados em (**) ,
. E assim a,b,c,d estarão bem determinados .
,
se exprimir por
onde
é uma das possibilidades
ou
e assim teremos
que contradiz o fato de
.

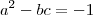 ,nesta época que respondi este tópico vi a mesma eq. como
,nesta época que respondi este tópico vi a mesma eq. como 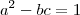 que em consequência nos
que em consequência nos  se
se 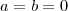 , a seguir vou rever minha resposta ].
, a seguir vou rever minha resposta ].  então
então 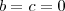 ? Caso sim ,note que a matriz
? Caso sim ,note que a matriz  se escreve como
se escreve como 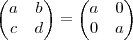 e deixando o número
e deixando o número  em evidência ,temos que
em evidência ,temos que 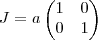 ou de forma mais compacta
ou de forma mais compacta  .Por hipótese a matriz
.Por hipótese a matriz  é tal que
é tal que 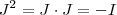 .
. 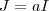 teremos
teremos 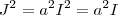 que é um absurdo , pois para qualquer número real
que é um absurdo , pois para qualquer número real  o seu quadrado será positivo e assim vemos que não existe
o seu quadrado será positivo e assim vemos que não existe  real p/ o qual
real p/ o qual 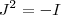 .
. não é real é pela equação que já foi mencionada entre[]
não é real é pela equação que já foi mencionada entre[] 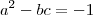 .Com
.Com  temos
temos  .
.


