As matrizes A, I e J são quadradas de ordem 2 e I é a matriz identidade. Se a matriz A =
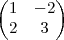 satisfaz as relações
satisfaz as relações 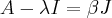 e
e 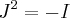 , com
, com  e
e  números reais, então a matriz J é igual a:
números reais, então a matriz J é igual a:Resposta:
![J=+ ou - \frac{1}{\sqrt[]{3}}
\begin{pmatrix}
-1 & -2 \\
2 & 1
\end{pmatrix} J=+ ou - \frac{1}{\sqrt[]{3}}
\begin{pmatrix}
-1 & -2 \\
2 & 1
\end{pmatrix}](/latexrender/pictures/c62514c673a86917f6b5e6e2ea624f7b.png)

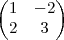 satisfaz as relações
satisfaz as relações 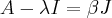 e
e 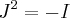 , com
, com  e
e  números reais, então a matriz J é igual a:
números reais, então a matriz J é igual a:![J=+ ou - \frac{1}{\sqrt[]{3}}
\begin{pmatrix}
-1 & -2 \\
2 & 1
\end{pmatrix} J=+ ou - \frac{1}{\sqrt[]{3}}
\begin{pmatrix}
-1 & -2 \\
2 & 1
\end{pmatrix}](/latexrender/pictures/c62514c673a86917f6b5e6e2ea624f7b.png)

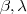 com os termos da matriz inversa de
com os termos da matriz inversa de  .Nota a matriz
.Nota a matriz  tem determinante não nulo e assim ela possui inversa e esta matriz denotada por
tem determinante não nulo e assim ela possui inversa e esta matriz denotada por  é única .
é única .  então
então 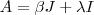 (1) .Multiplicando-se (1) por
(1) .Multiplicando-se (1) por 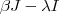 e usando
e usando  no lado esquerdo da igualdade e
no lado esquerdo da igualdade e 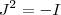 no lado direito ,obtemos
no lado direito ,obtemos 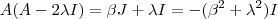 (2) . Logo ,
(2) . Logo ,  e assim concluímos que
e assim concluímos que 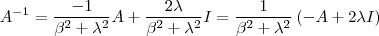 (3) .
(3) .
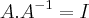 para descobrir os escalares. Como
para descobrir os escalares. Como  ,
,  e
e  , teríamos:
, teríamos:![\begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}
\left[ \frac{1}{{\beta}^{2}+{\lambda}^{2}}\left(-A + 2\lambda I \right) \right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix} \begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}
\left[ \frac{1}{{\beta}^{2}+{\lambda}^{2}}\left(-A + 2\lambda I \right) \right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}](/latexrender/pictures/501f688f5cc5d82b82842ada85d5b873.png)
![\begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}
\left[ \frac{1}{{\beta}^{2}+{\lambda}^{2}}\left(-
\begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}
\right) + 2\lambda I \right) \right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix} \begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}
\left[ \frac{1}{{\beta}^{2}+{\lambda}^{2}}\left(-
\begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}
\right) + 2\lambda I \right) \right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}](/latexrender/pictures/198b718a00ea39b73341b677c16fdf46.png)
![\begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}\left[\frac{1}{{\beta}^{2}+{\lambda}^{2}}\left(
\begin{pmatrix}
-1 & 2 \\
-2 & -3
\end{pmatrix}
\right) +
\begin{pmatrix}
2\lambda & 0 \\
0 & 2\lambda
\end{pmatrix}
\right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix} \begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}\left[\frac{1}{{\beta}^{2}+{\lambda}^{2}}\left(
\begin{pmatrix}
-1 & 2 \\
-2 & -3
\end{pmatrix}
\right) +
\begin{pmatrix}
2\lambda & 0 \\
0 & 2\lambda
\end{pmatrix}
\right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}](/latexrender/pictures/d48f64f33893203438310a00d4527205.png)
![\begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}\left[\frac{1}{{\beta}^{2}+{\lambda}^{2}}
\begin{pmatrix}
2\lambda-1 & 2 \\
-2 & 2\lambda+3
\end{pmatrix}
\right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix} \begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}\left[\frac{1}{{\beta}^{2}+{\lambda}^{2}}
\begin{pmatrix}
2\lambda-1 & 2 \\
-2 & 2\lambda+3
\end{pmatrix}
\right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}](/latexrender/pictures/f970343077885c2f6d6865686bf7bda9.png)
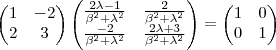

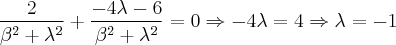
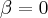

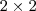 não singulares que nos fornece esta matriz através da aplicação de uma fórmula . (veja : http://pt.wikipedia.org/wiki/Matriz_inv ... s_2.C3.972) .
não singulares que nos fornece esta matriz através da aplicação de uma fórmula . (veja : http://pt.wikipedia.org/wiki/Matriz_inv ... s_2.C3.972) . ![A\left[ \frac{1}{\beta^2 + \lambda^2}(-A+ 2\lambda I) A\right] = I A\left[ \frac{1}{\beta^2 + \lambda^2}(-A+ 2\lambda I) A\right] = I](/latexrender/pictures/cbc041bc731d574b16f6772bc0ba5e08.png) que pode ser desenvolvida da seguinte forma :
que pode ser desenvolvida da seguinte forma : 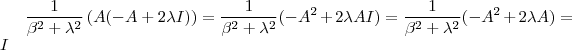 .
.  vamos obter
vamos obter 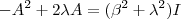 . Como
. Como 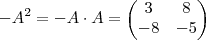 ,
,  e
e 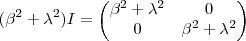 ,segue
,segue 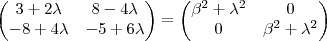 .
. 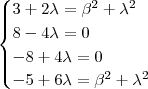 .
. 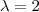 e assim o sistema se reduz a
e assim o sistema se reduz a  que nos dá
que nos dá 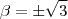 como solução .
como solução .  ,substituindo os escalares pelos valores encontrados obterá a reposta .
,substituindo os escalares pelos valores encontrados obterá a reposta .

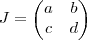 . Pelo que
. Pelo que 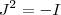 ,segue
,segue 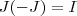 . Portanto
. Portanto  é invertível e sua inversa é
é invertível e sua inversa é  (*)
(*) 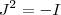 acarreta que
acarreta que 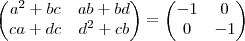 e assim
e assim 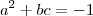
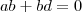

 ,
,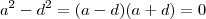

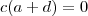 .
.  ou
ou  .Se ocorrer
.Se ocorrer  implicará
implicará 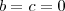 e
e  .Já na segunda possibilidade , temos
.Já na segunda possibilidade , temos 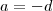 ,para este caso devemos encontrar
,para este caso devemos encontrar  reais que cumpre
reais que cumpre 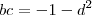 (**) e
(**) e  (Apenas dividi por \beta e definir os novos escalares como m e p ) . Prosseguindo :
(Apenas dividi por \beta e definir os novos escalares como m e p ) . Prosseguindo : 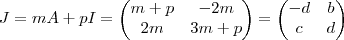 . Logo ,
. Logo ,  (1)
(1)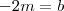 (2)
(2) 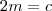 (3)
(3) (4) ,
(4) , 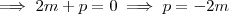 .
.  . Utilizando estes resultados em (**) ,
. Utilizando estes resultados em (**) , 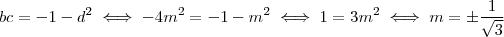 . E assim a,b,c,d estarão bem determinados .
. E assim a,b,c,d estarão bem determinados .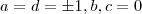 ,
, se exprimir por
se exprimir por 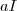 onde
onde  é uma das possibilidades
é uma das possibilidades  ou
ou  e assim teremos
e assim teremos 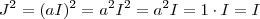 que contradiz o fato de
que contradiz o fato de 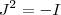 .
. 
 implicará
implicará 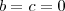 e
e  ". Pode esclarecer?
". Pode esclarecer?santhiago escreveu:Há outra forma . Suponha. Pelo que
,segue
. Portanto
é invertível e sua inversa é
(*)
. Além disso,acarreta que
e assim
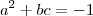
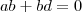

,
equivalentemente ,

.
Analisando as soluções p/ primeira equação concluímos queou
.Se ocorrer
implicará
e
.Já na segunda possibilidade , temos
,para este caso devemos encontrar
reais que cumpre
(**) e
(Apenas dividi por \beta e definir os novos escalares como m e p ) . Prosseguindo :
. Logo ,
(1)
(2)
(3)
(4) ,
[(1) +(4)].
Então. Utilizando estes resultados em (**) ,
. E assim a,b,c,d estarão bem determinados .
Para aquele primeiro caso em que,
se exprimir por
onde
é uma das possibilidades
ou
e assim teremos
que contradiz o fato de
.
Editado .

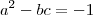 ,nesta época que respondi este tópico vi a mesma eq. como
,nesta época que respondi este tópico vi a mesma eq. como 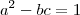 que em consequência nos
que em consequência nos  se
se 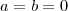 , a seguir vou rever minha resposta ].
, a seguir vou rever minha resposta ].  então
então 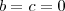 ? Caso sim ,note que a matriz
? Caso sim ,note que a matriz  se escreve como
se escreve como 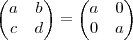 e deixando o número
e deixando o número  em evidência ,temos que
em evidência ,temos que 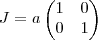 ou de forma mais compacta
ou de forma mais compacta  .Por hipótese a matriz
.Por hipótese a matriz  é tal que
é tal que 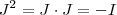 .
. 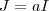 teremos
teremos 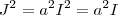 que é um absurdo , pois para qualquer número real
que é um absurdo , pois para qualquer número real  o seu quadrado será positivo e assim vemos que não existe
o seu quadrado será positivo e assim vemos que não existe  real p/ o qual
real p/ o qual 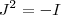 .
. não é real é pela equação que já foi mencionada entre[]
não é real é pela equação que já foi mencionada entre[] 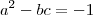 .Com
.Com  temos
temos  .
.



Voltar para Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)