Da folha circular corta-se setor circular de modo que se obtenha o funil conforme mostra a figura abaixo. Se o funil tem volume máximo, então o ângulo central
 , em radianos, é igual a:
, em radianos, é igual a:A resposta é:
![2\pi\sqrt[]{\frac{2}{3}} 2\pi\sqrt[]{\frac{2}{3}}](/latexrender/pictures/9b41d8f6c1b1866e9c8345bf4b7f48d3.png)
Eu cheguei na seguinte expressão para o volume do cone:
![V=\frac{\pi{R}^{3}}{3}\left(\frac{2\pi-\alpha}{2\pi} \right)^{2}\sqrt[]{1-\left(\frac{2\pi-\alpha}{2\pi} \right)^{2}} V=\frac{\pi{R}^{3}}{3}\left(\frac{2\pi-\alpha}{2\pi} \right)^{2}\sqrt[]{1-\left(\frac{2\pi-\alpha}{2\pi} \right)^{2}}](/latexrender/pictures/746004ab1a52f6bbb05bf3e135c6e87b.png)
Chamei
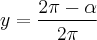 , e reescrevi assim:
, e reescrevi assim: ![y=\frac{\pi{R}^{3}}{3}{y}^{2}\sqrt[]{1-{y}^{2}} y=\frac{\pi{R}^{3}}{3}{y}^{2}\sqrt[]{1-{y}^{2}}](/latexrender/pictures/7c84505e51fa66e1cc41345f7f53460c.png) , com
, com 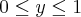
Derivando obtive o ponto de máximo
![y=\sqrt[]{\frac{2}{3}} y=\sqrt[]{\frac{2}{3}}](/latexrender/pictures/e215c3380230385cd0a4ec5d34f1aedf.png)
Pois bem, já fiz um monte de cálculos e não chego no gabarito. Para chegar na fórmula do volume eu fiz assim:
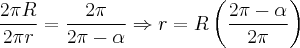 e o H eu tirei por Pitágoras.
e o H eu tirei por Pitágoras.Não sei se fiz certo, pois considerei o meu cone obtido a partir da parte branca (já que subtraio
 ) se é aqui que está meu erro, como consertá-lo e encontrar a resposta do gabarito?
) se é aqui que está meu erro, como consertá-lo e encontrar a resposta do gabarito?

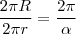
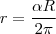



 , avisa que eu resolvo.
, avisa que eu resolvo.

